20-06-2024 23:01

Status :

Tags : mathematics algebra linear algebra Matrix

Determinants

With every square matrix A of ordern, we associate a determinant of order n which is denoted by $\det (A)or|A|$

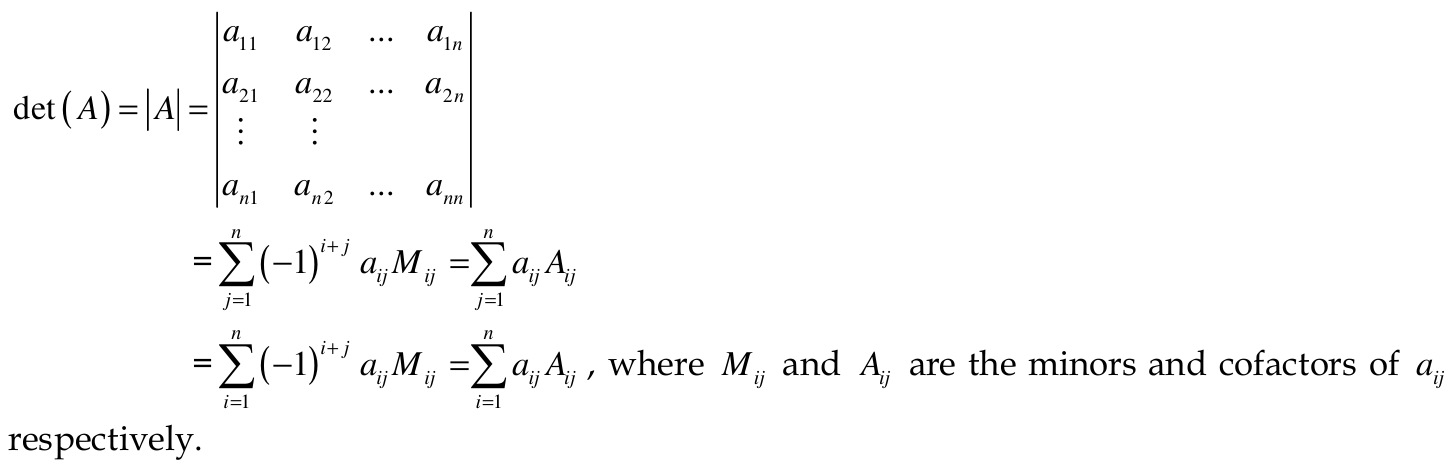
Properties of determinants

• If all the elements of a row (or column) are zero then the value of the determinant is zero.
• If any two rows (or columns) are interchanged, then the value of the determinant is multiplied by (—1) .
• If the corresponding elements of two rows (or columns) are proportional to each other, then the value of the determinant is zero.
• If each element of a row or column is multi lied b a scalar a then the value of the determinant is multiplied by the scalar a.
• If is a factor of each element of a row (or a column) then this factor can be taken out of the determinant.
• If a non-zero constant multiple of the elements of some row (or column) is added to the corresponding elements of some other row (or column), then the value of the determinant remains unchanged.
• In general, $|A+B|\ne |A|+|B|$

References