Signals and Systems LTI Convolution Sum

Representation of Discrete Time Signal in terms of Impulses

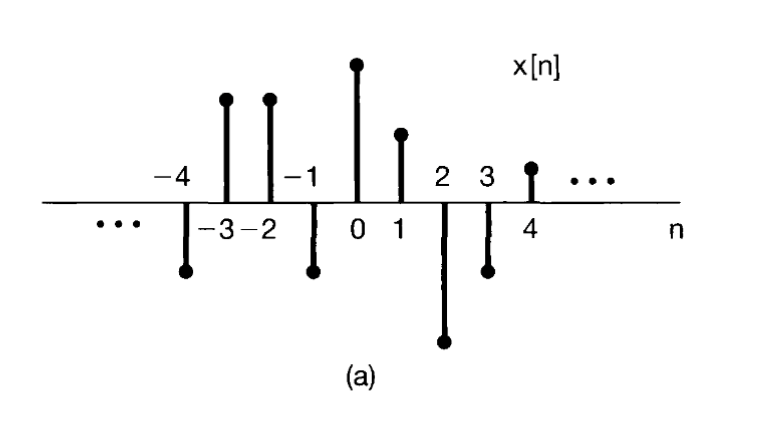
As we have already understood that Unit Impulse Signal is one of the key building blocks of the signals one should also know that they can build any signal with the help of just this. For example

Example

First $x[n]$ is defined by

$\begin{array}{r}x[n]=..+x[-3]\delta [n+3]+x[-2]\delta [n+2]+x[-1]\delta [n+1]+x[0]\delta [n]\\ +x[1]\delta [n-1]+x[2]\delta [n-2]+x[3]\delta [n-3]+...\end{array}$ Thus we can write $x[n]={\sum }_{k=-\infty }^{+\infty }x[k]\delta [n-k].$ Now we look at this other expression derived from this $x[n]$

$x[-1]\delta [n+1]=\{\begin{array}{ll}x[-1],& n=-1\\ 0,& n\ne -1\end{array},$

Given expression:

$$x[-1]\delta [n+1]=\{\begin{array}{ll}x[-1],& n=-1\\ 0,& n\ne -1\end{array}$$

Step 1: Understanding the Delta Function

The discrete-time unit impulse function (or delta function) is defined as:

$$\delta [n]=\{\begin{array}{ll}1,& n=0\\ 0,& n\ne 0\end{array}$$

This means that $\delta [n+1]$ is a shifted version of $\delta [n]$, given by:

$$\delta [n+1]=\{\begin{array}{ll}1,& n=-1\\ 0,& n\ne -1\end{array}$$

Step 2: Multiply by ( $x[-1]$ )

Multiplying by a constant ( $x[-1]$ ) results in:

$$x[-1]\delta [n+1]=\{\begin{array}{ll}x[-1]\cdot 1=x[-1],& n=-1\\ x[-1]\cdot 0=0,& n\ne -1\end{array}$$

Conclusion:

This is exactly what is given in the problem statement:

$$x[-1]\delta [n+1]=\{\begin{array}{ll}x[-1],& n=-1\\ 0,& n\ne -1\end{array}$$

Thus, the result is derived by recognizing that $\delta [n+1]$ is nonzero only when ( n = -1 ), and multiplying it by ( x[-1] ).

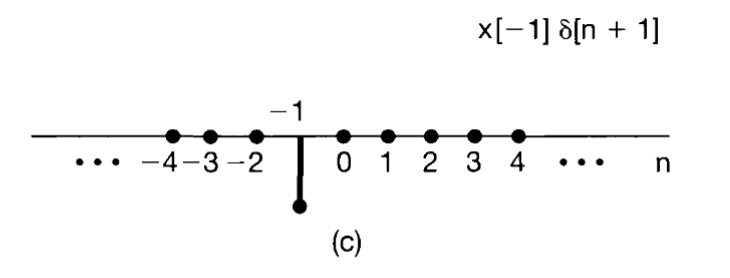
Convolution

Summary Note on Impulse Response $h[n]$ and Convolution of Discrete Signals

---

What is $h[n]$?

• Impulse Response $h[n]$ represents the output of a system when the input is a unit impulse function $\delta [n]$, which is a signal that is 1 at $n=0$ and 0 everywhere else.
• Definition: The impulse response tells us how a system responds to a unit impulse over time. It is a fixed characteristic of a linear time-invariant (LTI) system, meaning it does not change with time.

How is $h[n]$ Defined?

• The impulse response $h[n]$ is defined for all time indices $n$, but in some cases, it may be non-zero only at specific points. For example: $$h[n]=\{1,1,1\},\text{ for }n=0,1,2$$ This means the system responds with 1 at $n=0$, 1 at $n=1$, and 1 at $n=2$. All other values of $h[n]$ are 0.

Resolution of Convolution

• The impulse response $h[n]$ can be thought of as defining the resolution of the convolution process. This means that the length of $h[n]$ dictates how many past and future points the system “sees” when calculating the output.
  • If $h[n]$ is defined for only 3 points (like $n=0,1,2$), the system has a narrow resolution and only takes into account 3 points of past and future input values when performing the convolution.

Relevance of $h[n]$ to $x[n]$

• $x[n]$ is the input signal, and $h[n]$ defines how the system responds to the input.
• The convolution operation combines $x[n]$ with $h[n]$ to produce the output $y[n]$. The system’s response to every point of $x[n]$ depends on the values of $h[n]$ at corresponding time shifts.

---

Convolution Formula and Symbolic Representation

The output $y[n]$ of a system is calculated using the convolution of the input signal $x[n]$ and the system’s impulse response $h[n]$. The formula is:

$$y[n]=\sum _{k=-\infty }^{\infty }x[k]h[n-k]$$

• Convolution Symbolically: $y[n]$ is the output signal at time $n$, computed by summing the products of the input values $x[k]$ and the corresponding shifted impulse response $h[n-k]$.
• Shifted Impulse Response: The term $h[n-k]$ means that the impulse response is shifted by $k$ for each point in the summation, considering past and future values of $x[k]$.

---

Example:

Let’s use the following simple example to illustrate:

• Input signal $x[n]$: $\{1,2,3\}$ for $n=0,1,2$
• Impulse response $h[n]$: $\{1,1,1\}$ for $n=0,1,2$

Now, let’s compute $y[2]$.

$$y[2]=\sum _{k=-\infty }^{\infty }x[k]h[2-k]$$

We only need to consider the values of $x[k]$ and $h[2-k]$ for $k=0,1,2$ because those are the only non-zero values for $x[n]$ and $h[n]$.

• For $k=0$: $x[0]=1$, $h[2-0]=h[2]=1$, so this contributes $1\times 1=1$
• For $k=1$: $x[1]=2$, $h[2-1]=h[1]=1$, so this contributes $2\times 1=2$
• For $k=2$: $x[2]=3$, $h[2-2]=h[0]=1$, so this contributes $3\times 1=3$

Thus:

$$y[2]=1+2+3=6$$

---

Future Example:

Now let’s consider a future example where the impulse response $h[n]$ still has 3 points, but we will calculate the output for a later value of $y[4]$.

Let’s assume:

• Input signal $x[n]$: $\{1,2,3,0,4,5\}$ for $n=0,1,2,3,4,5$
• Impulse response $h[n]$: $\{1,1,1\}$ for $n=0,1,2$

We want to calculate $y[4]$.

$$y[4]=\sum _{k=-\infty }^{\infty }x[k]h[4-k]$$

Now, compute the contributions:

• For $k=0$: $x[0]=1$, $h[4-0]=h[4]=0$, so this contributes $1\times 0=0$
• For $k=1$: $x[1]=2$, $h[4-1]=h[3]=0$, so this contributes $2\times 0=0$
• For $k=2$: $x[2]=3$, $h[4-2]=h[2]=1$, so this contributes $3\times 1=3$
• For $k=3$: $x[3]=0$, $h[4-3]=h[1]=1$, so this contributes $0\times 1=0$
• For $k=4$: $x[4]=4$, $h[4-4]=h[0]=1$, so this contributes $4\times 1=4$

Thus:

$$y[4]=0+0+3+0+4=7$$

---

Conclusion:

• Impulse Response $h[n]$: It is the system’s response to a unit impulse $\delta [n]$. It is a fixed property of the system, defining how the system reacts over time.
• The length of $h[n]$ defines the resolution of convolution: the number of points in $x[n]$ that contribute to the output $y[n]$ is determined by how long $h[n]$ is.
• The convolution formula $y[n]={\sum }_{k=-\infty }^{\infty }x[k]h[n-k]$ combines the input signal $x[n]$ with the shifted impulse response $h[n-k]$ to generate the output signal $y[n]$.

To provide a similar approach to the one found in Oppenheim’s “Signals and Systems” book, let’s structure the continuous-time signal representation and convolution in a manner that aligns with the book’s style. Oppenheim’s book is known for its clear and detailed explanations, often accompanied by illustrative examples and step-by-step derivations.

---

Representation of Continuous-Time Signals in Terms of Impulses

Continuous-Time Unit Impulse Function

The continuous-time unit impulse function, denoted as $\delta (t)$, is a fundamental concept in signal processing. It is defined as:

$$\delta (t)=\{\begin{array}{ll}\infty ,& t=0\\ 0,& t\ne 0\end{array}$$

with the integral property:

$${\int }_{-\infty }^{\infty }\delta (t)dt=1$$

This function is crucial because it allows us to represent any signal as a sum of scaled and shifted impulses.

Representation of a Continuous-Time Signal

Any continuous-time signal $x(t)$ can be expressed as an integral of impulses:

$$x(t)={\int }_{-\infty }^{\infty }x(\tau )\delta (t-\tau )d\tau$$

This equation indicates that $x(t)$ can be constructed by integrating over all time shifts $\tau$ of the impulse function $\delta (t)$, each scaled by the value of $x(\tau )$.

---

Convolution in Continuous-Time Systems

Impulse Response $h(t)$

The impulse response $h(t)$ of a continuous-time system is the output of the system when the input is a unit impulse $\delta (t)$. It characterizes the system’s response to an impulse over time and is a fundamental property of linear time-invariant (LTI) systems.

Convolution Formula

The output $y(t)$ of a continuous-time system is given by the convolution of the input signal $x(t)$ and the impulse response $h(t)$:

$$y(t)={\int }_{-\infty }^{\infty }x(\tau )h(t-\tau )d\tau$$

This formula shows that the output $y(t)$ is obtained by integrating the product of the input signal $x(\tau )$ and the shifted impulse response $h(t-\tau )$ over all time shifts $\tau$.

Example

Let’s consider an example to illustrate the convolution in continuous-time systems, similar to the approach in Oppenheim’s book.

• Input signal $x(t)$: A rectangular pulse defined as:

  $$x(t)=\{\begin{array}{ll}1,& 0\le t\le 1\\ 0,& \text{otherwise}\end{array}$$

• Impulse response $h(t)$: An exponential decay defined as:

  $$h(t)=\{\begin{array}{ll}{e}^{-t},& t\ge 0\\ 0,& t<0\end{array}$$

To find the output $y(t)$, we compute the convolution:

$$y(t)={\int }_{-\infty }^{\infty }x(\tau )h(t-\tau )d\tau$$

For $0\le t\le 1$, the convolution integral becomes:

$$y(t)={\int }_0^t{e}^{-(t-\tau )}d\tau =e^{-t}{\int }_0^t{e}^{\tau }d\tau =e^{-t}{\left[e^{\tau }\right]}_0^t=e^{-t}(e^t-1)=1-e^{-t}$$

For $t>1$, the convolution integral becomes:

$$y(t)={\int }_0^1{e}^{-(t-\tau )}d\tau =e^{-t}{\int }_0^1{e}^{\tau }d\tau =e^{-t}{\left[e^{\tau }\right]}_0^1=e^{-t}(e-1)$$

Thus, the output $y(t)$ is:

$$y(t)=\{\begin{array}{ll}1-e^{-t},& 0\le t\le 1\\ (e-1)e^{-t},& t>1\end{array}$$

---

Conclusion

• The continuous-time unit impulse function $\delta (t)$ is essential for representing continuous-time signals.
• The impulse response $h(t)$ characterizes the system’s response to an impulse input.
• The convolution formula for continuous-time systems combines the input signal $x(t)$ with the shifted impulse response $h(t-\tau )$ to produce the output signal $y(t)$.

This structured approach aligns with the detailed and illustrative style found in Oppenheim’s “Signals and Systems” book. If you need further elaboration or additional examples, feel free to ask!

Continuous

References

Information

• date: 2025.02.12
• time: 22:22