Computer Organization and Lecture 19

Sequential Logic Circuits

• Memory exists
• Registers
  • Group of flip flops
  • Holds information
• Counters
  • A register that goes through a predetermined sequence of states

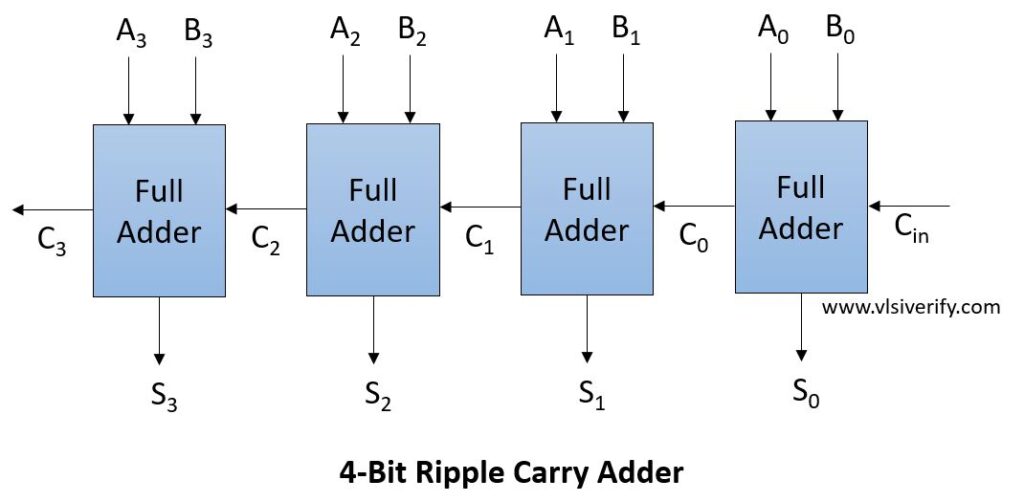
High speed adders

Assume that a sequential full adder takes 5 nano seconds to calculate addition. Then the next will take 10 ns. This cascading time is too huge for a sequential circuit.

gantt
    title Sequential Full Adder Timing
    dateFormat  X
    axisFormat %s ns

    section Addition Process
    First Addition  :done, 0, 5
    Second Addition :done, 0, 10
    Third Addition  :done, 0, 15
    Fourth Addition :done, 0, 20

To solve this problem we have carry look ahead adder that fetches $c_0$, $c_1$, $c_2$, $c_3$. The k map equations for carry look ahead is as follows. $C_{i+1}=a_i.b_i+(a_i)$ Here are the equations for a Carry Look-Ahead Adder (CLA):

1. Generate and Propagate:

$$ $$Pi=Ai⊕BiP_i = A_i \oplus B_i$$ 2. **Carry Equations:** $$ Ci+1=Gi+(Pi⋅Ci)$$ $$ C_{i+1} = G_i + (P_i \cdot C_i) $$ $$ C_1 = G_0 + (P_0 \cdot C_0) $$ $$ C_2 = G_1 + (P_1 \cdot C_1) $$

$C_3=G_2+(P_2\cdot C_2)$ $C4=G3+(P3\cdot C3)$

3. Sum Equation:

$Si=Pi\oplus Ci{S}_i=P_i\oplus C_i$

8087 Math Co Processors

• Specially designed to do quick complex mathematical calculations
• Implemented to reduce work load on main processor
• 8087 Shares same resources as the main
• Has 60 new instructions
• all new pneumonies begin with “F”/“E” to diff from main instructions

References

Information

• date: 2025.03.11
• time: 08:35