Continued from Signals & System Transformation of the independent variable
Prerequisites : Eulers Formula
Continuous-Time Complex Exponential and Sinusoidal Signals
In this section We introduce several basic continuous-time and discrete-time signals. Not only do these signals occur frequently, but they also serve as basic building blocks from which we can construct many other signals.
The continuous-time complex exponential signal is of the form where and are, in general, complex numbers. Depending upon the values of these parameters, the complex exponential can exhibit several different characteristics.
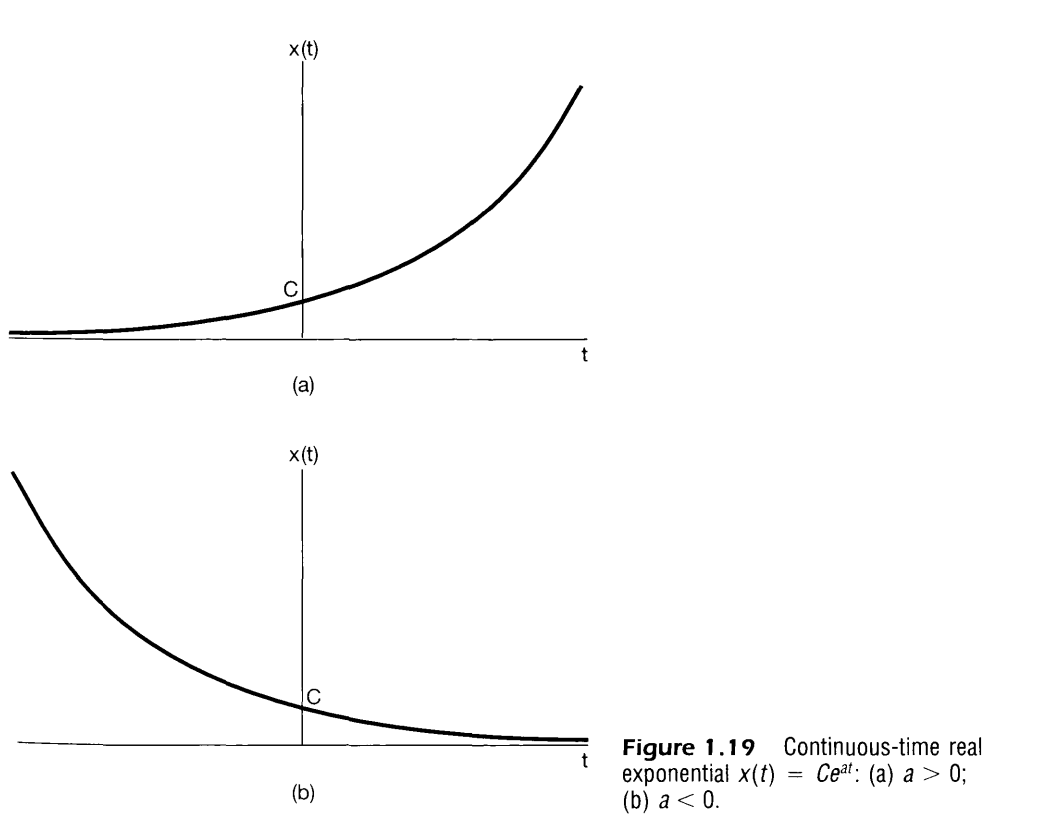
Real Exponential Signals
if and are real (in which case x(t) is called a real exponential), there are basically two types of behavior.
If a is positive, then as t increases x(t) is a growing exponential, a form that is used in describing many different physical processes, including chain reactions in atomic explosions and complex chemical reactions.
If a is negative, then x(t) is a decaying exponential, a signal that is also used to describe a wide variety of phenomena, including the process of radioactive decay and the responses of RC circuits and damped mechanical systems.
Periodic Complex Exponential and Sinusoidal Signals
For Continuous
Complex exponentials is obtained by constraining a to be purely imaginary. here , Which is the frequency of the signal
If this signal was to be periodic referring Periodicity Then it shall follow this rule of Periodic Signals
Cancelling out the common terms.
it follows that for periodicity, we must have
thus by simply putting the angular frequency we can say that which makes this function periodic for any T.
But if then the fundamental period of will be given as such
and and are constant
This is because and then we can shift eqn to make the above one.
Sinusodials
A signal closely related to the periodic complex exponential is the sinusoidal signal.
This is because of Euler’s formulae. ( no need for deep understanding but cool if you can study )
Writing One eqn in other forms.
We can write the equation in the Exponential part as
similarly we can write the Sinusodial Part as an Exponent
Thus we can say that where means the real part and as the imaginary part
Fundamental Time Period
Just keep in mind that is Inversely proportional to this is simply because and . So Changing one affects the otthers
Energy Signals & Periodic signals
Consider the periodic ex- ponential signal of eq. (1.21), and suppose that we calculate the total energy and average power in this signal over one period:
Thus they are important examples of signals with infinite total energy but finite average power.
Applications
complex exponential signals are also used to describe the characteristics of many physical processes-in particular, physical systems in which energy is conserved. For example, as shown in Problem 2.61, the natural response of an LC circuit is sinusoidal, as is the simple harmonic motion of a mechanical system consisting of a mass connected by a spring to a stationary support. The acoustic pressure variations corresponding to a single musical tone are also sinusoidal.
Periodic complex exponentials will play a central role in much of our treatment of signals and systems, in part because they serve as extremely useful building blocks formany other signals. We will often find it useful to consider sets of harmonically related complex exponentials—that is, sets of periodic exponentials, all of which are periodic with a common period . Specifically, a necessary condition for a complex exponential to be periodic with period To is that
Examples
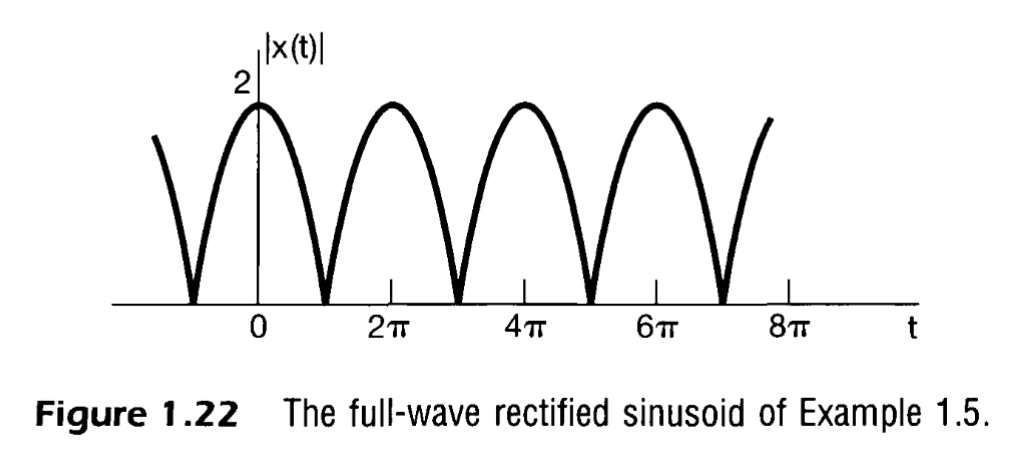
Example 1.5
Sometimes we write signal eqns as a sum of two complex exponentials as the product of a single complex exponent and a single sinusoid. For example, suppose we wish to plot the magnitude of the signal
We can use the law of indices to perform this operation
and with Euler’s formulae To calculate the magnitude we can do for any the magnitude of is ( Since Z is a rotating complex vector in complex plane and the coefficient multiplied to it is the magnitude. Imagine graphically. )
General Complex Exponential Signals
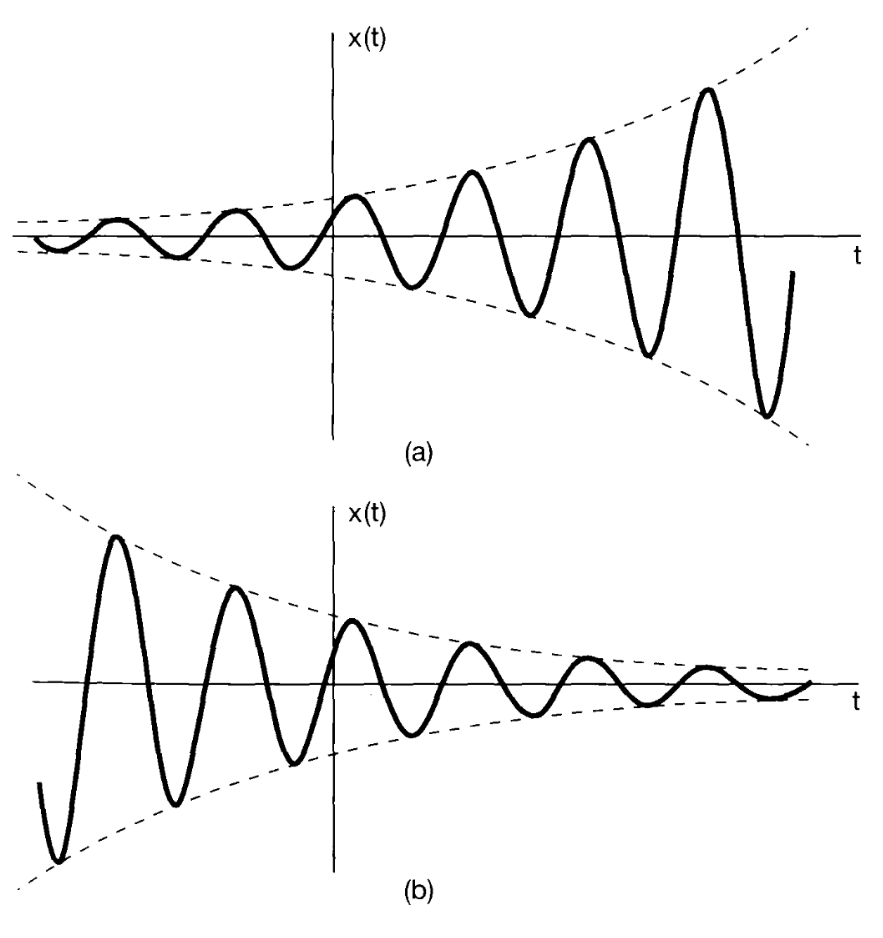
The most general case of a complex exponential can be expressed and interpreted in terms of the two cases we have examined so far: the real exponential and the periodic complex exponential. Specifically, consider a complex exponential where is expressed in polar form and a in rectangular form. That is,
and
Then
Thus by Euler’s Relation we can boil this down to
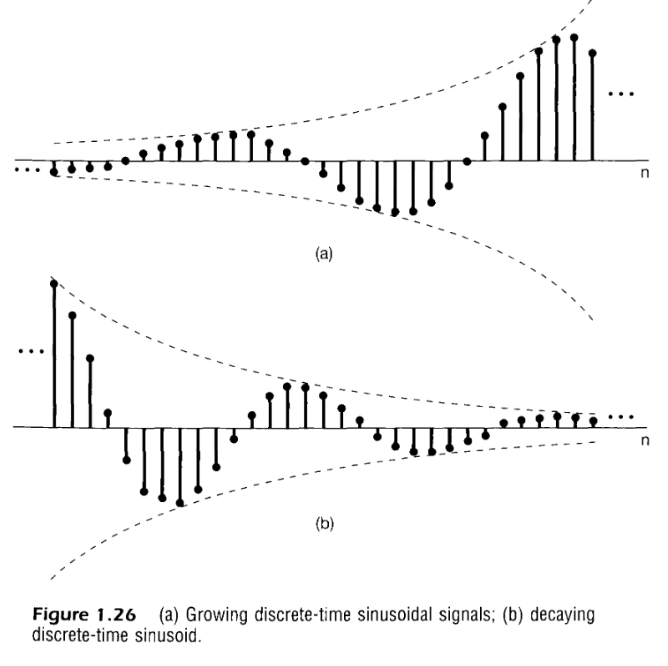
Thus we can say that for the real and imaginary part of this eqn is sinusoidal. For we can say that the sinusoidal is exponentially growing and For we can say that the sinusoidal is exponentially decaying
The graph depicts these properties.
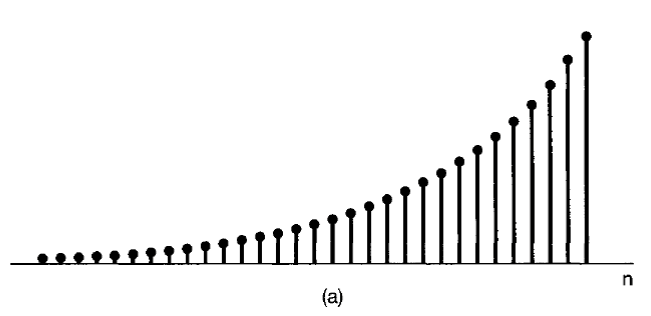
Discrete
If and are real we can have one of several types of behaviour, as illustrated in. if the magnitude of the signal grows exponentially with , while if we have a decaying exponential
Complex Exponential Equation
For a discrete based equation the function can be given as. Its graphical Representation is as follows
 calculate
we can calculate the value of fundamental time period
calculate
we can calculate the value of fundamental time period
Complex Sinusoidal
This eqn is closely related to the eqn
and thus we can similar write the eqn as we did with sinusodial continous and then get this
Periodicity of Complex Exponentials
Consider the following literal . If we evaluate this expression we get. Thus we can conclude that every
Information
- date: 2024.08.20
- time: 02:49
- Continued to Signals and Systems Unit Impulse and Unit Step Functions