Expression Tree
An Expression Tree is a binary tree used to represent expressions involving variables, constants, and operators. Each node in the tree represents either an operator or an operand, and the structure of the tree reflects the order of operations in the expression.
Key Characteristics:
-
Internal Nodes:
- Represent operators like
+,-,*,/. - Typically binary operators (with two children), but can include unary operators (with one child).
- Represent operators like
-
Leaf Nodes:
- Represent operands (constants or variables, such as
2,x, etc.).
- Represent operands (constants or variables, such as
-
Binary Tree Structure:
- Operators form the internal nodes, and operands form the leaves.
- Higher-precedence operators are deeper in the tree, closer to the leaves.
-
Order of Operations:
- The tree structure naturally respects operator precedence (multiplication and division are handled before addition and subtraction).
-
Evaluation:
- Recursively evaluate the expression tree by evaluating subtrees (starting from the leaves), applying operators in the correct order.
Example Expression: (3 + 4) * (5 - 2)
The corresponding expression tree:
*
/ \
+ -
/ \ / \
3 4 5 2
- The root (
*) represents multiplication, with+and-as its operands. - The leaf nodes (
3,4,5,2) are constants.
Traversals:
- Inorder (Left, Root, Right): Produces an infix expression, e.g.,
((3 + 4) * (5 - 2)). - Preorder (Root, Left, Right): Produces a prefix expression, e.g.,
* + 3 4 - 5 2. - Postorder (Left, Right, Root): Produces a postfix expression, e.g.,
3 4 + 5 2 - *.
Example: Postfix Expression 53-4*9+
To construct the expression tree for the postfix expression 53-4*9+, follow these steps:
- Process each character in the postfix expression:
- If the character is an operand, push it onto a stack.
- If it’s an operator, pop two nodes from the stack, create a new node with the operator, and set the two popped nodes as its children.
- Push the new subtree back onto the stack.
Step-by-Step Example:
For the postfix expression 53-4*9+:
- Process
5,3→ push operands onto the stack. - Process
-→ pop5and3, create a subtree(- 5 3). - Process
4→ push operand onto the stack. - Process
*→ pop-subtree and4, create(* (- 5 3) 4). - Process
9→ push operand onto the stack. - Process
+→ pop*subtree and9, create(+ (* (- 5 3) 4) 9).
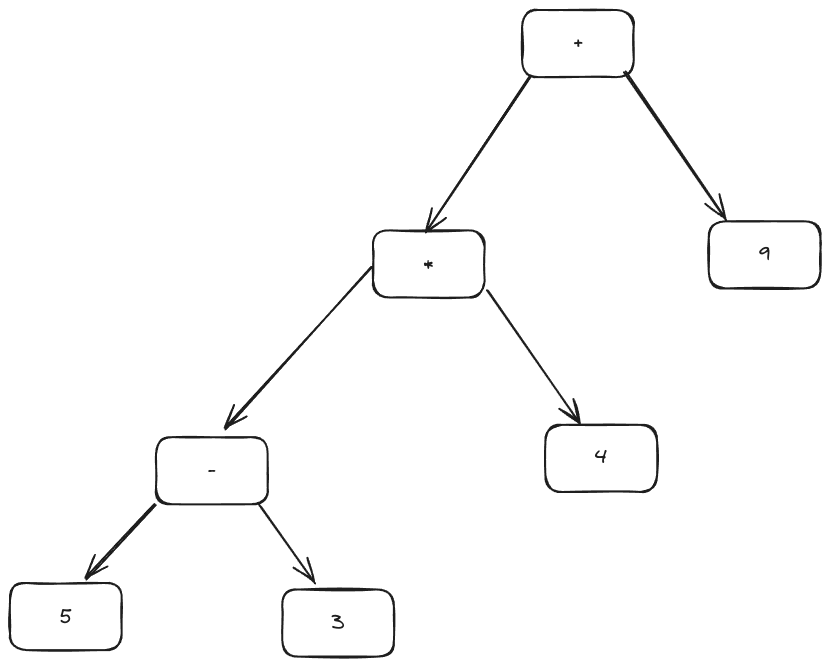
The final expression tree is:
+
/ \
* 9
/ \
- 4
/ \
5 3
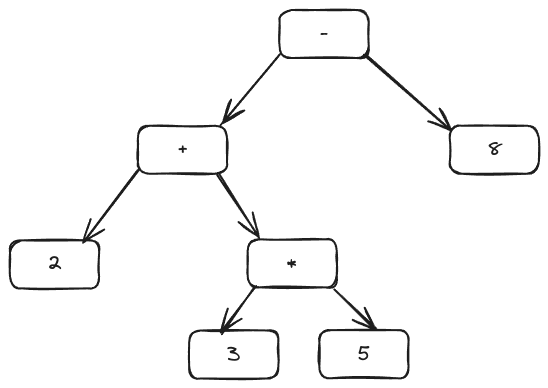
Example for Expression 235*+8-:
The expression 235*+8- can be processed similarly using the same stack-based approach to produce an expression tree.
Code Snippet to Evaluate the Expression Tree:
function evaluate(tree) {
if (tree is a leaf) {
return value of the operand;
} else {
let operator = tree.operator;
let leftVal = evaluate(tree.left);
let rightVal = evaluate(tree.right);
return apply operator to leftVal and rightVal;
}
}Conclusion:
Expression trees are an efficient way to represent and evaluate arithmetic expressions, respecting the order of operations by their structure. They are widely used in compilers, interpreters, and symbolic computation.
Huffmans Tree
A Huffman Tree is a specific type of binary tree used in Huffman coding, an algorithm for lossless data compression. The tree is constructed based on the frequency of each character in the data, where frequently occurring characters are assigned shorter binary codes and less frequent characters are assigned longer codes. This results in a compressed binary encoding of the data.
Key Characteristics of a Huffman Tree:
-
Binary Tree Structure:
- Each character in the data is represented as a leaf node in the tree.
- Internal nodes do not represent characters; they represent the combined frequency of their child nodes.
-
Frequency-Based Construction:
- Characters with higher frequencies are positioned closer to the root, resulting in shorter binary codes.
- Characters with lower frequencies are further from the root, leading to longer binary codes.
-
Prefix-Free Property:
- The binary codes generated by a Huffman Tree are prefix-free, meaning no code is a prefix of another. This allows the encoded message to be uniquely decodable without needing delimiters.
Steps to Construct a Huffman Tree:
-
Calculate Frequencies: Count the frequency of each character in the data.
-
Create Leaf Nodes: Create a leaf node for each character with its frequency and place all nodes in a priority queue (or min-heap) sorted by frequency.
-
Build the Tree:
- Remove the two nodes with the lowest frequency from the priority queue.
- Create a new internal node with a frequency equal to the sum of the two nodes’ frequencies.
- Set the two nodes as children of the new node, and add the new node back into the priority queue.
- Repeat until there is only one node left in the queue; this node is the root of the Huffman Tree.
-
Generate Codes:
- Assign binary codes to each character by traversing the tree from the root.
- Moving left adds a
0to the code, and moving right adds a1. - Each character’s binary code is formed by the path taken to reach its leaf node.
Example of Huffman Tree Construction:
Consider the string “BBAACCCCDD”.
-
Calculate Frequency:
B: 2, A: 2, C: 4, D: 2 -
Create Leaf Nodes and Initialize Priority Queue:
Nodes in queue (frequency): B(2), A(2), D(2), C(4) -
Build the Tree:
- Combine B(2) and A(2) to create an internal node with frequency 4.
- Nodes now: D(2), (BA)(4), C(4).
- Combine D(2) and (BA)(4) to create a new internal node with frequency 6.
- Nodes now: C(4), ((BA)D)(6).
- Combine C(4) and ((BA)D)(6) to create the root node with frequency 10.
-
Generate Codes:
Root / \ C (BA)D / \ BA D / \ B ACodes:
C = 0B = 101A = 100D = 11
Applications of Huffman Tree:
- Data Compression: Huffman coding reduces the size of files by replacing fixed-length codes with variable-length codes.
- Network Protocols: Used in protocols like JPEG, PNG, and MP3 for efficient data encoding.
- Efficient Data Transmission: Huffman coding reduces bandwidth usage by compressing data for transmission.
Summary
The Huffman Tree is a binary tree used in compression algorithms to generate efficient, prefix-free binary codes for characters based on their frequency. By assigning shorter codes to frequent characters and longer codes to infrequent ones, it achieves a high level of compression in data storage and transmission.
Weighted Binary Tree
A Weighted Binary Tree is a type of binary tree in which each node carries a specific weight or value that impacts various calculations, such as determining the optimal structure of the tree, prioritizing nodes, or calculating the overall cost of traversing or processing the tree. The concept of a weighted binary tree is often used in data compression, optimal search trees, and scheduling applications, where node weights guide the tree’s structure and traversal paths.
Key Characteristics of a Weighted Binary Tree:
-
Node Weights:
- Each node in the tree has an associated weight, representing a value such as frequency, priority, or cost.
- Node weights typically guide the construction and structure of the tree, affecting its shape and traversal patterns.
-
Weighted Path Length:
- The weighted path length is a measure of the total cost associated with accessing or processing all nodes in the tree.
- It is the sum of the products of each node’s weight and its depth in the tree. The depth is the distance from the root node to the node itself.
-
Balanced vs. Optimal Structure:
- In a weighted binary tree, nodes with higher weights are often closer to the root to reduce access or traversal cost, as accessing nodes deeper in the tree adds to the total path length.
- The goal is to minimize the total weighted path length by carefully arranging the nodes based on their weights.
Common Types of Weighted Binary Trees:
-
Huffman Tree:
- A special type of weighted binary tree used in Huffman coding for data compression.
- The tree is built based on character frequencies, where nodes with lower weights (frequencies) are deeper in the tree, and higher-weight nodes are closer to the root, creating a prefix-free code.
-
Optimal Binary Search Tree (OBST):
- A weighted binary tree used in search algorithms where nodes represent search keys.
- Weights represent the frequency or probability of each key being accessed.
- The tree structure is optimized to minimize the expected search time, so frequently accessed nodes are closer to the root.
-
Binary Heap:
- Although not a traditional binary tree, a binary heap is a type of weighted binary tree used in priority queues.
- Nodes are arranged based on weights, either in ascending or descending order (min-heap or max-heap).
- It maintains the heap property, where each parent node has a priority (weight) based on its relationship to its children.
Applications of Weighted Binary Trees:
-
Data Compression: Weighted binary trees like Huffman Trees are used to generate optimal prefix codes, reducing file sizes by minimizing the weighted path length of frequently used characters.
-
Efficient Searching: Optimal Binary Search Trees (OBST) enable faster searches by positioning frequently accessed elements near the root, which minimizes search costs in applications like databases.
-
Priority Queues and Scheduling: Binary heaps, a variant of weighted binary trees, are used in scheduling systems to manage tasks based on priority or frequency of access.
Example of Weighted Path Length Calculation:
Suppose we have a weighted binary tree with the following structure and weights:
(10)
/ \
(20) (30)
/ \ \
(40) (50) (60)
-
Weights:
- Root node = 10
- Left child of root = 20
- Right child of root = 30
- Leaf nodes: 40, 50, 60
-
Depths:
- Root node depth = 0
- Depth 1: 20, 30
- Depth 2: 40, 50, 60
-
Weighted Path Length Calculation:
The total weighted path length of the tree is 350, representing the cost of accessing all nodes based on their weights and depths.
Summary
A Weighted Binary Tree is a structured way of arranging nodes based on assigned weights, which guide the tree’s construction, traversal, and search efficiency. Examples like Huffman Trees and Optimal Binary Search Trees showcase how weighting improves performance, with applications in compression, efficient data retrieval, and task prioritization.
Continue to Data Structures & Algorithm Lecture 24