Continued from Probability and Statistics Lab 5
This lab is a direct application of the Binomial Distribution and Poisson Distribution in lectures.
To learn the functions and concepts of R Studio, read Binomial and Poisson’s distribution using R Studio.
Document - P6_Continuous probability distribution.pdf
Explanation Code For Class Problem
# Simulating 51 coin tosses
# X: Number of heads observed
# Generate possible values for X
x = c(0:51)
# Probability mass function (PMF)
# dbinom(x, size, prob, log = FALSE)
# x : Number of successes (heads)
# size : Number of trials (coin tosses)
# prob : Probability of success in each trial
# log : If TRUE, returns log probability
pmf = dbinom(x, 51, 0.5)
# Cumulative distribution function (CDF)
# pbinom(q, size, prob, lower.tail = TRUE, log.p = FALSE)
# q : Number of successes (heads)
# size : Number of trials (coin tosses)
# prob : Probability of success in each trial
# lower.tail : If TRUE, returns P(X ≤ q); if FALSE, returns P(X > q)
# log.p : If TRUE, returns log probability
cdf = pbinom(x, 51, 0.5)
# Combine values into a matrix
# cbind(...) combines vectors column-wise
cbind(x, pmf, cdf)
# Plot PMF
# plot(x, y, type = "p", main, xlab, ylab)
# x : X values
# y : Y values (probabilities)
# type : Plot type ('p' for points, 'l' for lines)
# main : Title of the plot
# xlab : Label for X-axis
# ylab : Label for Y-axis
plot(x, pmf)
# Plot CDF
plot(x, cdf)
## QUESTION 2
# Cumulative probability of X ≤ 40
pbinom(40, 51, 0.5)
## QUESTION 3
# Probability of X > 23 (1 - P(X ≤ 23))
1 - pbinom(23, 51, 0.5)
pbinom(23, 51, 0.5, lower.tail = FALSE)
ppois(16, lambda=12) # lower tail
ppois(16, lambda=12, lower=FALSE) Questions
Question 1
The probability of entering students in chartered accountant will graduate is 0.5. Determine the probability that out of 10 students i. None ii. One iii. At least one will graduate nb
# The probability of entering students in chartered accountant
# will graduate is 0.5. Determine the probability that out of 10
# students
## i. None
## ii. One
## iii. At least one
# None
dbinom(0,10,0.5)
# One
dbinom(1,10,0.5)
# At least one passes
pbinom(1,10,0.5,lower.tail = FALSE)> dbinom(0,10,0.5)
[1] 0.0009765625
> > # One
> dbinom(1,10,0.5)
[1] 0.009765625
> > # At least one passes
> pbinom(1,10,0.5,lower.tail = FALSE)
[1] 0.9892578Question 2
Find binomial distribution if the mean is 5 and variance is 10/3. Write a R program for above problem. Also write a R program to plot probability distribution and cumulative probability distribution.
Solution
# Problem: Find binomial distribution if the mean is 5 and
# variance is 10/3.
#
# Given:
# - Mean (μ) = 5
# - Variance (σ²) = 10/3
#
# Formulae:
# - Mean (μ) = n * p
# - Variance (σ²) = n * p * (1 - p) = n * p * q (where q = 1 - p)
# From Solving the equations we get
# n = 5, p=1/3
x=c(0:15)
result = pbinom(x,15,0.5)
plot(x,result)> > # From Solving the equations we get
> # n = 5, p=1/3
> x=c(0:15)
> result = pbinom(x,15,0.5)
> plot(x,result)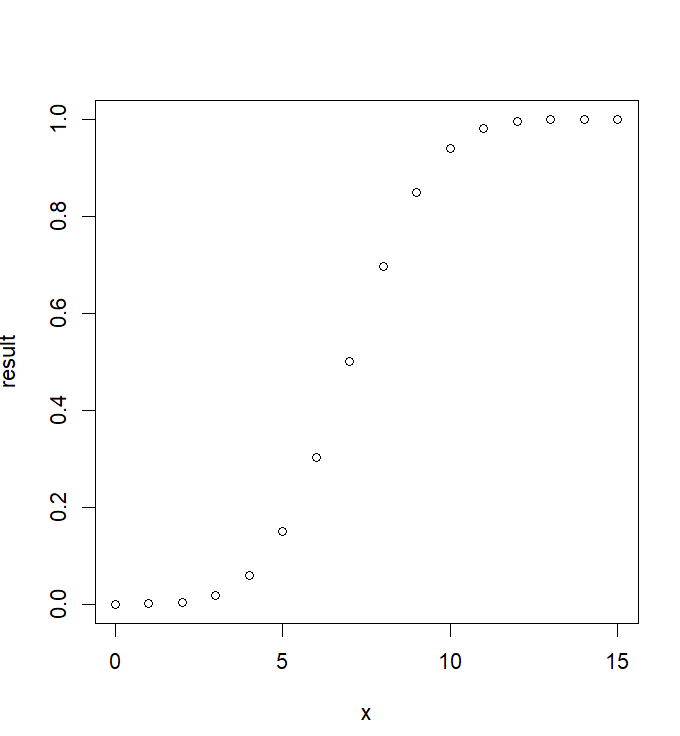
Question 3
The number of traffic accidents that occur on a particular stretch of road during a month follows a Poisson distribution with a mean of 7.6. Find the probability that
- less than three accidents will occur next month on this stretch of road.
- Exactly three accidents will occur next month on this stretch of road.
# Question 3: Poisson Distribution Problem
# The number of traffic accidents that occur on a particular stretch of road during a month
# follows a Poisson distribution with a mean of 7.6.
# Task:
# 1. Find the probability that less than three accidents will occur next month on this stretch of road.
# 2. Find the probability that exactly three accidents will occur next month on this stretch of road.
# Lambda (mean) is given as 7.6.
# To find the probability for each task, we will use the Poisson distribution formula:
# P(X = k) = (lambda^k * e^(-lambda)) / k!
# where 'lambda' is the mean (7.6) and 'k' is the number of accidents.
# Part 1: Probability of less than three accidents (X < 3)
# We will calculate P(X = 0), P(X = 1), and P(X = 2) and sum them to find P(X < 3)
# Part 2: Probability of exactly three accidents (X = 3)
# We will calculate P(X = 3) using the Poisson distribution formula.
x=c(0:31)
ppois(3,7.6)
dpois(3,7.6)
x=c(0:31)
> ppois(3,7.6)
[1] 0.05537128
> dpois(3,7.6)
[1] 0.03661436Question 4
Find 8 random values from a sample of 150 with probability of 0.4.
## Find 8 random values from a sample of 150 with probability of 0.4.
# Parameters
n = 150 # Total number of trials
size = 8 # Number of random values to generate
prob = 0.4 # Probability of success
# Generate 8 random values from a binomial distribution with 150 trials and probability of 0.4
random_values = rbinom(size, n, prob)
# Print the random values
cat("8 random values from a sample of 150 with probability 0.4: ", random_values, "\n")
## Find 8 random values from a sample of 150 with probability of 0.4.
> # Parameters
> n = 150 # Total number of trials
> size = 8 # Number of random values to generate
> prob = 0.4 # Probability of success
> > # Generate 8 random values from a binomial distribution with 150 trials and probability of 0.4
> random_values = rbinom(size, n, prob)
> > # Print the random values
> cat("8 random values from a sample of 150 with probability 0.4: ", random_values, "\n")
8 random values from a sample of 150 with probability 0.4: 64 63 60 65 58 53 62 56Question 5
How many heads will have a probability of 0.25 when a coin is tossed 51 times? What is the probability of getting 26 or fewer heads from 51 tosses of a coin?
Solution:
# Number of heads corresponding to 25% probability
qbinom(0.25, 51, 0.5)
# Probability of getting 26 or fewer heads
pbinom(26, 51, 0.5)Expected Output:
> qbinom(0.25, 51, 0.5)
[1] 23
> pbinom(26, 51, 0.5)
[1] 0.727937This means that the 25th percentile for the number of heads is 23, and the probability of getting 26 or fewer heads is approximately 72.8%.
Handwritten Solutions
References
Information
- date: 2025.02.18
- time: 12:33





