Signals and Systems Unit Impulse and Unit Step Functions

Continued from Signals and Systems Exponentials and Sinusoidals

Signals & Systems Unit Impulse and Unit Step Functions

We will look at the unit impulse and step functions in continuous and discrete time.

Discrete Unit Impulse & Step

Unit Pulse

One of the simplest discrete-time signals is the unit impulse (or unit sample), which is defined as $\delta [n]=\{\begin{array}{ll}0,& n\ne 0\\ 1,& n=0\end{array}$

Unit Step

A second basic discrete-time signal is the discrete-time unit step, denoted by $u[n]$ and defined by $u[n]=\{\begin{array}{ll}0,& n<0\\ 1,& n\ge 0\end{array}.$

Inter relation between Unit Pulse and Unit Step

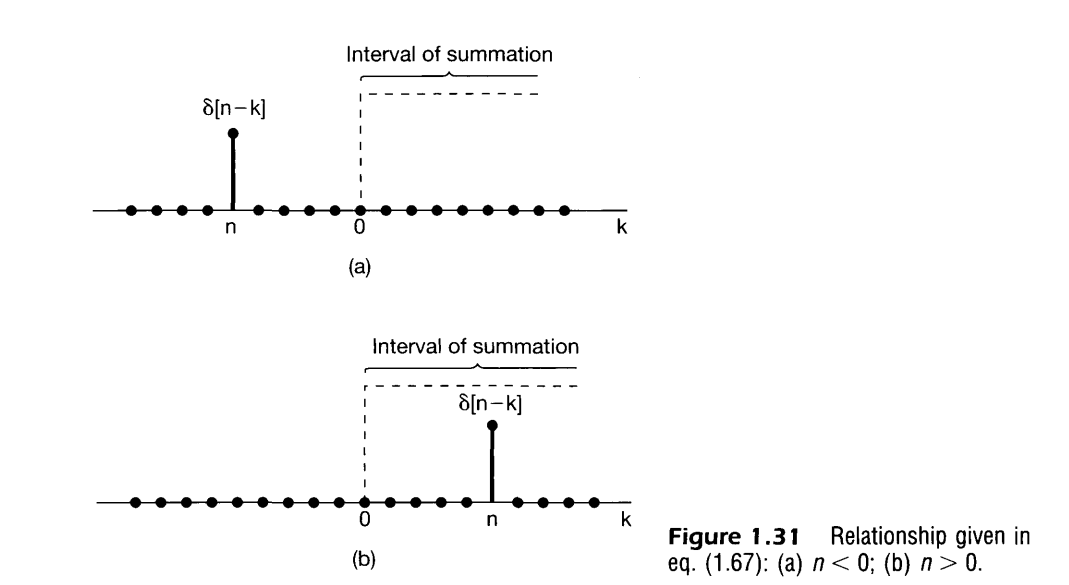
There is a close relationship between the discrete-time unit impulse and unit step. In particular, the discrete-time unit impulse is the first difference of the discrete-time step $\delta [n]=u[n]-u[n-1].$ Conversely, the discrete-time unit step is the running sum of the unit sample. That is, $u[n]={\sum }_{m=-\infty }^n\delta [m].$ To understand first one must realize that the summation value will at most be 1 and not greater than that. This is because the sigma function is defined such. refer Unit Impulse. Now when the value is 0 it sums up all the values from $-\infty$ to 0 and gets 1 for $u[0]$. When the value is 1 it sums up all the values from $-\infty$ to 0 and gets 1 for $u[1]$.

Furthermore, by changing the variable of summation from $m$ to $k=n-m$ We get $u[n]={\sum }_{k=\infty }^0\delta [n-k],$

Continuous Unit Impulse & Step

Unit Impulse

We already can conclude that the unit impulse can be same for both the functions since it only has a value at one point. So for that.

One of the simplest discrete-time signals is the unit impulse (or unit sample), which is defined as $\delta [n]=\{\begin{array}{ll}0,& n\ne 0\\ 1,& n=0\end{array}$

Link to original

Unit Step

The continuous-time unit step function $u(t)$ is defined in a manner similar to its discrete time counterpart. Specifically, $u(t)=\{\begin{array}{ll}0,& t<0\\ 1,& t>0\end{array},$ to the relationship between the discrete-time unit impulse and step functions. In particular, the continuous-time unit step is the running integral of the unit impulse $u(t)={\int }_{-\infty }^t\delta (\tau )d\tau .$ This also suggests a relationship between $\delta (t)$ and $u(t)$ analogous to the expression for $\delta [n]$ the continuous-time unit impulse can be thought of as the first derivative of the continuous-time unit step: $\delta (t)=\frac{du(t)}{dt}.$

Formally Unsolvable

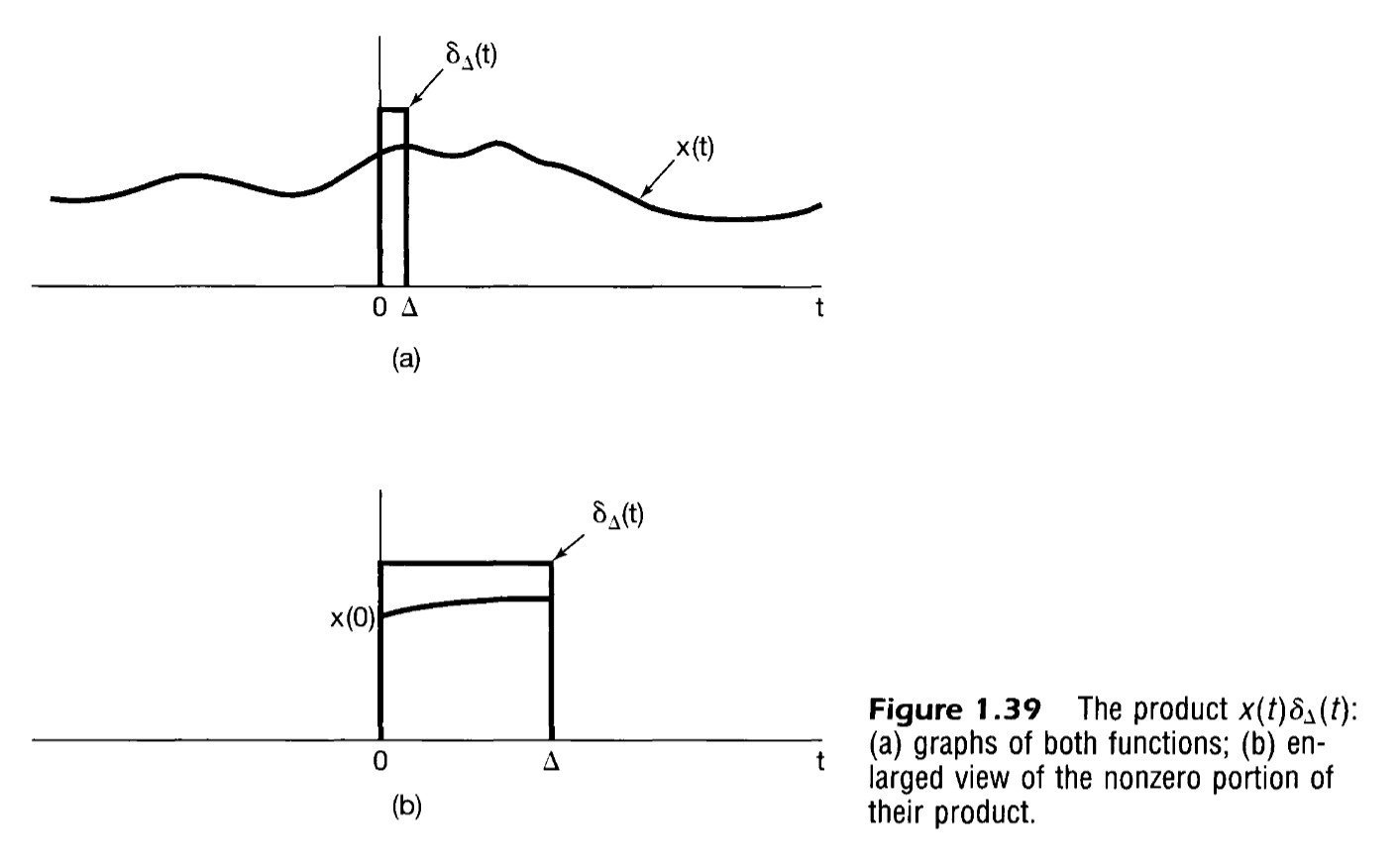
In contrast to the discrete-time case, there is some formal difficulty with this equation as a representation of the unit impulse function, since $u(t)$ is discontinuous at $t=0$ and consequently is formally not differentiable. We can, however, interpret eq. above by considering an approximation to the unit step $u_{\nabla }(t)$, as illustrated in Figure below , which rises from the value 0 to the value 1 in a short time interval of length $\nabla$. The unit step, of course, changes values instantaneously and thus can be thought of as an idealization of $u_{\nabla }(t)$, for $\nabla$ so short that its duration doesn’t matter for any practical purpose. Formally, $u(t)$ is the limit of $U_{\nabla }(t)$ as Ll ~ 0. Let us now consider the derivative

${\delta }_{\Delta }(t)=\frac{d{u}_{\Delta }(t)}{dt},$

Not So Important part

For a scaled unit impulse ${\int }_{-\infty }^{t}k\delta (\tau )d\tau =ku(t).$ and Multiplication of two functions in a function $x(t){\delta }_{\Delta }(t)\approx x(0){\delta }_{\Delta }(t).$

References

Information

• date: 2024.08.20
• time: 04:24
• Continued from Signals & System Continuous and Discrete Time Systems