Signals and Systems Properties of Linear Time Invariant Systems

Properties of Linear Time-Invariant (LTI) Systems

The Commutative Property

A basic property of convolution in both continuous and discrete time is that it is a commutative operation. This means that the order in which the input signal and the impulse response are convolved does not affect the output.

Discrete Time

In discrete time, the commutative property is expressed as:

$$x[n]\ast h[n]=h[n]\ast x[n]=\sum _{k=-\infty }^{+\infty }h[k]x[n-k]$$

Continuous Time

In continuous time, the commutative property is expressed as:

$$x(t)\ast h(t)=h(t)\ast x(t)={\int }_{-\infty }^{+\infty }h(\tau )x(t-\tau )d\tau$$

These expressions can be verified by substituting variables, showing that the roles of $x[n]$ and $h[n]$ (or $x(t)$ and $h(t)$) are interchangeable. This property is crucial in understanding that the output of an LTI system remains the same regardless of whether the input signal or the impulse response is shifted and summed.

---

The Distributive Property

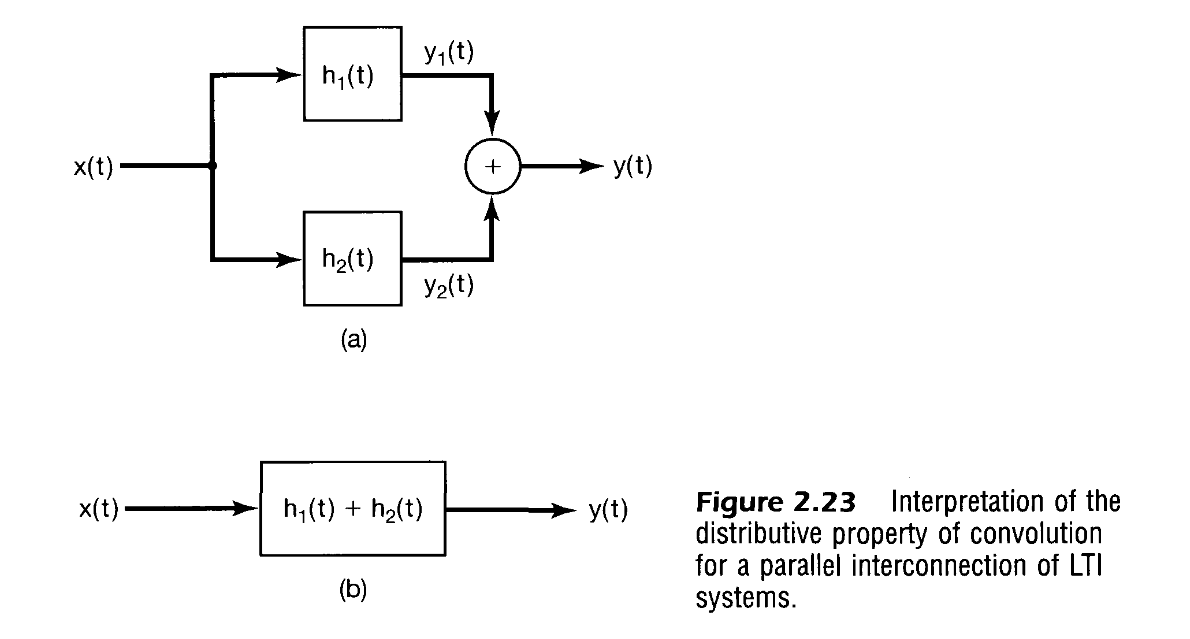
The distributive property is a fundamental characteristic of convolution in LTI systems, allowing for the separation and combination of signals in both discrete and continuous time domains.

Discrete Time

In discrete time, the distributive property is expressed as:

$$x[n]\ast (h_1[n]+h_2[n])=x[n]\ast h_1[n]+x[n]\ast h_2[n]$$

This property allows the convolution of an input signal with a sum of impulse responses to be computed as the sum of the individual convolutions.

Continuous Time

In continuous time, the distributive property is similarly expressed as:

$$x(t)\ast (h_1(t)+h_2(t))=x(t)\ast h_1(t)+x(t)\ast h_2(t)$$

This property is particularly useful in system analysis, as it allows for the decomposition of complex systems into simpler components, which can be analysed separately and then combined.

The distributive property simplifies the analysis and design of LTI systems by enabling the breakdown of convolution operations into more manageable parts, facilitating both theoretical understanding and practical implementation.

---

The Associative Property

Convolution also exhibits the associative property, which means that when convolving multiple signals, the order in which the convolutions are performed does not matter.

Discrete Time

For discrete-time systems, the associative property is given by:

$$x[n]\ast (h_1[n]\ast h_2[n])=(x[n]\ast h_1[n])\ast h_2[n]$$

Continuous Time

For continuous-time systems, the associative property is:

$$x(t)\ast (h_1(t)\ast h_2(t))=(x(t)\ast h_1(t))\ast h_2(t)$$

This property allows for the grouping of convolution operations, simplifying the analysis of systems with multiple stages.

---

LTI Systems with and without Memory

In the previous sections we have seen Systems with and without memory Now we will look their relevance with LTI Systems.

Systems with Memory

An LTI system is said to have memory if its output at any time depends not only on the current input but also on past or future inputs. This is typically the case for systems with an impulse response that extends over time. For example, a system described by a differential equation generally has memory.

Systems without Memory

An LTI system is memoryless if its output at any time depends only on the current input. Mathematically, this can be represented as:

$$y(t)=K\cdot x(t)$$

where $K$ is a constant. Memoryless systems are simpler to analyse because they do not require consideration of past or future inputs.

---

Invertibility of LTI Systems

An LTI system is invertible if it is possible to recover the input signal from the output signal. For a system to be invertible, it must have a stable and unique inverse system.

Conditions for Invertibility

1. Stability: The system must be stable, meaning that bounded inputs produce bounded outputs.
2. Minimum Phase: The system should not introduce any additional phase shifts that cannot be undone by the inverse system.
3. Non-zero Output: The system should not have zeros in its transfer function that cancel out the input, making recovery impossible.

Inverse System

The inverse of an LTI system is another LTI system that, when cascaded with the original system, produces the original input as the output. If $H(s)$ is the transfer function of the original system, then the transfer function of the inverse system is $H^{-1}(s)$.

---

Causality of LTI Systems

In the previous sections we have seen the meaning of Causality of a system. Now since this system is invariant with time we can relate this with the convolution property.

Definition

Causal Systems

A system is causal if the output at any time depends only on values of the input at the present time and in the past.

Such a system is called nonanticipative as they don’t look out for the future inputs.

For example a capacitor and resistor circuit would be causal as they only refer to the present and past values and don’t depend on future values. Refer Capacitor as an accumulator

All memory less systems are causal, since the output responds only to the current value of the input.

Examples of non causal systems

$y[n]=x[n]-x[n+1]$

Anti Causal

Anti causal signals is a special case of non causal where all the data is there only for $t\le 0$

Link to original

Mathematical Representation

For a causal system, the impulse response $h(t)$ must satisfy:

$$h(t)=0\text{for}t<0$$

This means that the impulse response is zero for all negative times, ensuring that the system does not respond to inputs before they occur.

Causality for a linear system is equivalent to the condition of initial rest; i.e., if the input to a causal system is 0 up to some point in time, then the output must also be 0 up to that time.

So, if $x[n]=0$, $y[n]=3$ $\ne 0$, so it does not satisfy the condition of initial rest.

Thus if $h(t)=0$ for $t<0$ then we can say that

$\nu [n]={\sum }_{k=-z}^{n}x[k]h[n-k],$ since till the point where the inputs were 0 so were the outputs if we apply commutative property we can also say $y[n]={\sum }_{k=()}^{{\phi }_{\circ }}h[k]x[n-k].$ Similarly for continuous $h(t)=0\mathrm{for}t<0,$ $y(t)={\int }_{-\infty }^{t}x(\tau )h(t-\tau )d\tau ={\int }_0^{\infty }h(\tau )x(t-\tau )d\tau .$

Stability of LTI Systems

A system is stable if for every bounded input there is a bounded output. To mathematically determine the stability we can use this expression. $\left|x[n]\right|<B\forall n.$ Suppose that we apply this input to an LTI system with unit impulse response h[n]. Then, using the convolution sum, we obtain an expression for the magnitude of the output: $|y[n]|=\left|{\sum }_{k=-\infty }^{+\infty }h[k]x[n-k]\right|.$ $|y[n]|\le {\sum }_{k=-\infty }^{+\infty }|h[k]||x[n-k]|.$ $\left|y[n]\right|\le B{\sum }_{k=-\infty }^{+\infty }\left|h[k]\right|\mathrm{for}\mathrm{all}n.$ ${\sum }_{k=-\infty }^{+\infty }|h[k]|<\infty ,$ Similarly for continuous ${\int }_{-\infty }^{+\infty }|h(\tau )|d\tau <\infty .$

References

Information

• date: 2025.02.13
• time: 03:45