Probability and Statistics Lecture 2

Continued from Probability and Statistics Lecture 1

Concepts used

Probability Core Concepts

Probability Spaces, Conditional Probability, and Independence

Probability Spaces

Consider an experiment whose outcome is not predictable with certainty. However, although the outcome of the experiment will not be known in advance, let us suppose that the set of all possible outcomes is known. This set of all possible outcomes of an experiment is known as the SAMPLE SPACE of the experiment and is denoted by $S$.

Example:

If the experiment consists of flipping two coins, then the sample space consists of the following four points: $S=\{HH,HT,TH,TT\}$

Each outcome in a sample space is called a Sample Point. Number of sample points in a sample space $S$ is denoted as $n(S)=nk$ where $n$ is the number of outcomes and $k$ is the number of objects.

Probability:

If an experiment results in $n$ exhaustive, mutually exclusive, and equally likely cases, and $m$ of them are favorable to the happening of an event $A$, then the probability of happening of event $A$ is:

$P(A)=\frac{m}{n}$

Since the number of cases in which the event $A$ will not happen is $n-m$, the probability that event $A$ will not happen is:

$P(\overline{A})=\frac{n-m}{n}$

Therefore,

$P(A)+P(\overline{A})=1$

Axioms of Probability:

Consider an experiment whose sample space is $S$. For each event $E$ of the sample space $S$, then the following axioms hold:

1. $0\le P(E)\le 1$
2. $P(S)=1$

---

Laws of Probability:

1. Addition Theorem:

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

If $A$ and $B$ are exclusive events, i.e., disjoint sets, then:

$P(A\cup B)=P(A)+P(B)$

2. Addition Theorem (for three events):

If $A$, $B$, and $C$ are pairwise exclusive events, then:

$P(A\cup B\cup C)=P(A)+P(B)+P(C)-P(A\cap B)-P(A\cap C)-P(B\cap C)+P(A\cap B\cap C)$

Complementary Event:

$P(A^c)=1-P(A)$

---

Conditional Probability and Independence

Conditional Probability:

If $A$ and $B$ are two events in a sample space $S$, then the probability of the event $A$ when the event $B$ has already occurred is called the conditional probability of $A$ and is denoted by $P(A|B)$ and defined as:

$P(A|B)=\frac{P(A\cap B)}{P(B)}$

The probability $P(A|B)$ is an updating of $P(A)$ based on the knowledge that event $B$ has already occurred.

Multiplication Law of Probability:

$P(A\cap B)=P(B|A)\cdot P(A)=P(A|B)\cdot P(B)$

Independent Events:

A set of events is said to be independent if the occurrence of any one of them does not depend on the occurrence or non-occurrence of the others. If two events $A$ and $B$ are independent, then:

$P(A\cap B)=P(A)\cdot P(B)$

---

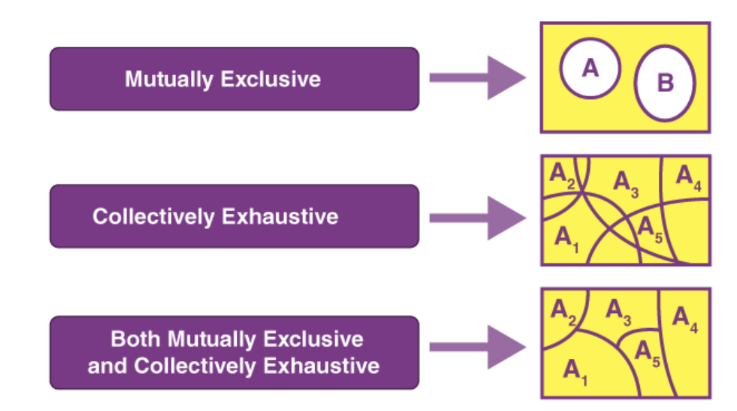
Mutually Exclusive and Collectively Exhaustive:

• Mutually Exclusive: Events cannot happen at the same time.
• Collectively Exhaustive: Events together make up everything that can possibly happen.
• Both Mutually Exclusive and Collectively Exhaustive: Events that both mutually exclude each other and together exhaust all possibilities.

---

Theorem of Total Probability:

If $B_1,B_2,\dots ,B_n$ are a set of exhaustive and mutually exclusive events and $A$ is another event associated with $B_i$, then:

$P(A)={\sum }_{i=1}^{n}P(B_i)\cdot P(A|B_i)$

Bayes’ Theorem:

If $B_1,B_2,B_3,\dots$ are mutually exclusive and exhaustive events with $P(B_i)\ne 0$ for $i=1$ to $n$ of a random experiment, then for any arbitrary event $A$ of the sample spaces of the above experiment with $P(A)>0$, we have:

$P(B_i|A)=\frac{P(B_i)\cdot P(A|B_i)}{{\sum }_{i=1}^{n}P(B_i)\cdot P(A|B_i)}$

References:

1. Probability, Statistics and Random Processes, T. Veerarajan, Tata McGraw Hill, 3rd edition.
2. Fundamentals of Mathematical Statistics, S.C. Gupta & V.K. Kapoor, Sultan Chand & Sons.

---

Multiplication Law of Probability:

For two events $A$ and $B$ in a sample space $S$, the multiplication law of probability states that:

$P(A\cap B)=P(B|A)\cdot P(A)=P(A|B)\cdot P(B)$

Independent Events:

A set of events is said to be independent if the occurrence of any one of them does not depend on the occurrence or non-occurrence of the others. If two events $A$ and $B$ are independent, then:

$P(A\cap B)=P(A)\cdot P(B)$

Example: Fair Dice Tossed

Find the probability of getting a 1 given that an odd number has been obtained.

Deck of Cards:

• A standard deck has 52 cards, divided equally into two colors: Red and Black.
• The deck consists of four suits: Spades, Hearts, Diamonds, and Clubs.
  • Hearts and Diamonds are Red; Spades and Clubs are Black.
• Each suit has 13 cards: Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King.

Problem:

A card is drawn from the deck. Find the following:

a. Probability of drawing a Queen:

$P(\text{Queen})=\frac{\text{Number of Queens}}{\text{Total number of cards}}=\frac{4}{52}$

b. Conditional Probability:

Find the conditional probability $P(\text{a Queen}|\text{a face card})$. Face cards are King, Queen, and Jack in each suit.

$P(\text{Queen}|\text{Face Card})=\frac{P(\text{Queen}\cap \text{Face Card})}{P(\text{Face Card})}$

c. Conditional Probability of drawing a Queen given the card is a Club:

$P(\text{Queen}|\text{Club})=\frac{P(\text{Queen}\cap \text{Club})}{P(\text{Club})}$

References

• Chat GPT with ma’ams note for source
• I was absent :P

References

Information

• date: 2025.02.18
• time: 22:42

Link to original

Ref

• Continued to Probability and Statistics Lecture 3

Information

• date: 2025.02.03
• time: 15:25