Theory of Total Probability

Law of Total Probability

The Law of Total Probability is a fundamental theorem in probability theory that relates marginal probabilities to conditional probabilities. It allows us to compute the probability of an event by considering all possible scenarios (partitions of the sample space) and using the conditional probabilities for each scenario.

Formula:

If $E_1,E_2,\dots ,E_n$form a partition of the sample space (i.e., the events $E_i$ are mutually exclusive and exhaustive), then the total probability of an event $A$ can be expressed as:

$$P(A)=\sum _{i=1}^{n}P(A\mid E_i)P(E_i)$$

Explanation:

• $P(A\mid E_i)$ is the conditional probability of $A$ given $E_i$.
• $P(E_i)$ is the probability of event $E_i$.
• The sum runs over all the possible events $E_1,E_2,\dots ,E_n$, which partition the entire sample space.

The law allows us to calculate $P(A)$ by considering how $A$ behaves across the different “parts” (or “cases”) defined by the partition $E_1,E_2,\dots ,E_n$.

Intuition:

Suppose you want to find the probability of event $A$, but directly calculating $P(A)$ is difficult. Instead, you break down $A$ based on different scenarios (events $E_1,E_2,\dots ,E_n$) that together cover all possibilities. You then calculate the conditional probability of $A$ given each scenario and combine these with the probabilities of the scenarios to find the total probability of $A$.

Example:

Suppose we want to calculate the probability that a randomly chosen person has a disease $D$. We can partition the population into two groups: those who are tested for the disease ($T$) and those who are not tested ($T^c$):

$$P(D)=P(D\mid T)P(T)+P(D\mid T^c)P(T^c)$$

Here, $P(D\mid T)$ is the probability of having the disease given that the person is tested, and $P(T)$ is the probability of being tested.

Extended Form:

If we have multiple partitions, the total probability can be generalized as:

$$P(A)=\sum _{i=1}^{n}P(A\mid E_i)P(E_i)$$

Where $E_1,E_2,\dots ,E_n$ form a partition of the sample space.

---

Theorem of Total Probability:

If $B_1,B_2,\dots ,B_n$ is a set of exhaustive and mutually exclusive events, and $A$ is another event associated with $B_i$, then

$P(A)={\sum }_{i=1}^{n}P(B_i)P(A|B_i)$

Mutually Exclusive: Two events $A$ and $B$ are mutually exclusive if

$A\cap B=\varnothing$

Exhaustive: A set of events $A_1,A_2,\dots ,A_n$ is exhaustive if

${\bigcup }_{i=1}^n{A}_i=S$

Example:

Let $S=\{1,2,3\}$, and

$A_1=\{1,2\},A_2=\{2,3\}$

The events are mutually exclusive and exhaustive because:

$A_1\cup A_2=S,A_1\cap A_2=\varnothing$

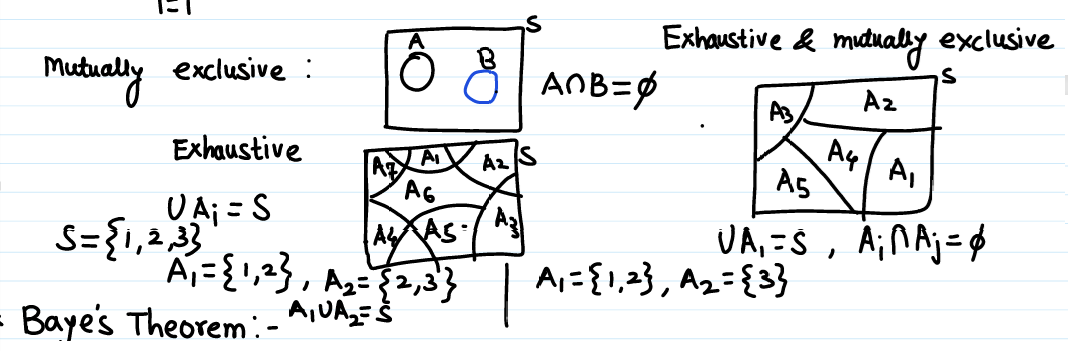
Example Question

Suppose there are three doors ( E_1, E_2, E_3 ) at your college, and there’s a zombie apocalypse. We want to calculate the probability of escaping through any of these doors.

Using the Theorem of Total Probability, the probability of escaping ( P(E) ) is:

$$P(E)=P(E_1)\cdot P(E\mid E_1)+P(E_2)\cdot P(E\mid E_2)+P(E_3)\cdot P(E\mid E_3)$$

Example Question Trick

Now, consider a more complex scenario: After escaping, what is the probability that the person escaped through door 2?

To solve this, we use Bayes’ Theorem, which we learned in a previous lecture. Bayes’ Theorem allows us to update our beliefs based on new evidence. The formula for Bayes’ Theorem is:

$$P(B_i\mid A)=\frac{P(B_i)\cdot P(A\mid B_i)}{P(A)}$$

Given that the person has escaped (event ( A )), the probability that they escaped through door 2 (event ( E_2 )) is:

$$P(E_2\mid E)=\frac{P(E_2)\cdot P(E\mid E_2)}{P(E)}$$

Where:

• ( P(E_2 \mid E) ) is the probability of having escaped through door 2 given that the person has escaped.
• ( P(E_2) ) is the prior probability of escaping through door 2.
• ( P(E \mid E_2) ) is the likelihood of escaping given that the person chose door 2.
• ( P(E) ) is the total probability of escaping, calculated using the Theorem of Total Probability.

Conclusion

The combination of the Theorem of Total Probability and Bayes’ Theorem provides a powerful framework for analyzing complex probabilistic scenarios. These theorems are fundamental in statistics and probability theory, with wide-ranging applications in fields such as machine learning, medical diagnosis, and risk assessment.

References

Information

• date: 2025.02.03
• time: 09:42