Introduction to Cryptography Lecture 7

Diffie Hellman Key Exchange

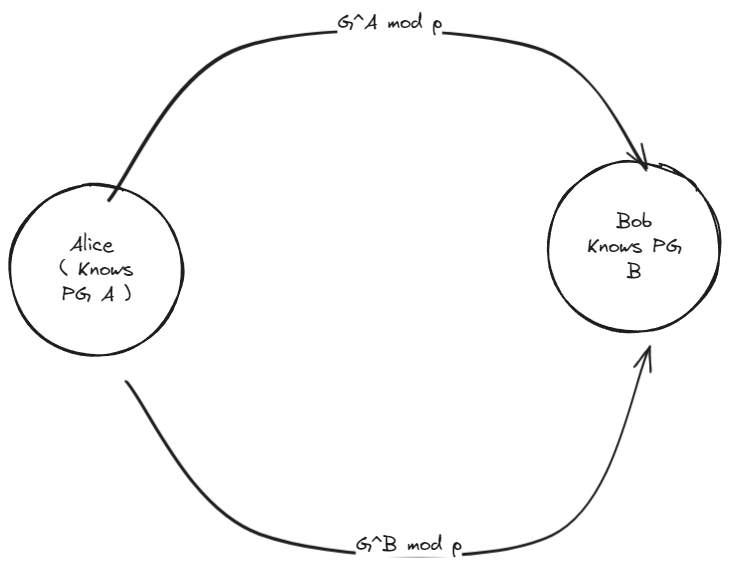
Alice and Bob agree on a prime number $p$ and a base $g$.

1. Alice chooses a secret number $a$ and sends Bob $g^a\mathrm{mod}p$
2. Bob chooses a secret number $b$ and sends Alice $g^b\mathrm{mod}p$
3. Alice computes $(g^b\mathrm{mod}p{)}^a\mathrm{mod}p$
4. Bob computes $(g^a\mathrm{mod}p{)}^b\mathrm{mod}p$

Example

Alice and Bob agree on:

• $p=23$
• $g=5$

Alice chooses $a=6$.

Alice’s Calculation:

• Alice computes her public key: $$A=g^a\mathrm{mod}p=5^6\mathrm{mod}23=15625\mathrm{mod}23=8$$
• Alice sends $A=8$ to Bob.

Bob’s Calculation:

• Bob chooses a secret number $b=15$.
• Bob computes his public key: $$B=g^b\mathrm{mod}p=5^{15}\mathrm{mod}23=30517578125\mathrm{mod}23=19$$
• Bob sends $B=19$ to Alice.

Shared Secret Calculation:

• Alice computes the shared secret using Bob’s public key:

  $$S=B^a\mathrm{mod}p=19^6\mathrm{mod}23=470427017\mathrm{mod}23=2$$

• Bob computes the shared secret using Alice’s public key:

  $$S=A^b\mathrm{mod}p=8^{15}\mathrm{mod}23=470427017\mathrm{mod}23=2$$

Thus, both Alice and Bob now share the same secret key $S=2$.

---

Diffie-Hellman with $p=19$ and $g=9$

1. Alice and Bob agree on:

   • $p=19$
   • $g=9$

2. Alice’s Secret Number:

   • Alice chooses $a=6$.

3. Alice’s Public Key:

   $$A=g^a\mathrm{mod}p=9^6\mathrm{mod}19$$

   Compute $9^6\mathrm{mod}19$.

4. Bob’s Secret Number:

   • Bob chooses $b$ (e.g., $b=12$).

5. Bob’s Public Key:

   $$B=g^b\mathrm{mod}p=9^{12}\mathrm{mod}19$$

   Compute $9^{12}\mathrm{mod}19$.

6. Shared Secret Computation:

   • Alice computes $S=B^a\mathrm{mod}p$.
   • Bob computes $S=A^b\mathrm{mod}p$.

Now, both Alice and Bob have a shared secret key they can use for encrypted communication.

---

RSA Encryption

the RSA (Rivest, Shamir, and Adleman) algorithm, which is a widely used asymmetric cryptographic algorithm. The content covers the key aspects of RSA, including the generation of keys.

Key Points from the Slide:

1. RSA Basics:

   • RSA involves a public key and a private key.
   • The public key is broadcasted and used for encrypting messages.

2. Key Generation Steps:

   • Choose two distinct prime numbers $p$ and $q$.
   • Compute $n=p\times q$, where:
     • $n$ is used as the modulus for both the public and private keys.
   • Compute Euler’s Totient Function, $\Phi (n)=(p-1)(q-1)$.

3. Algorithm Processes:

   • Key Generation
   • Encryption
   • Decryption

---