Signals & System Basic System Properties

We discuss the number of basic properties of continuous and discrete systems.

Systems with and without memory

Memoryless

A system is said to be memoryless if the output for each value of the independent variable depends on only on the input at that instance. $y[n]=(2x[n]-x^2[n]{)}^2$ A memoryless system is one where the output at any given moment depends solely on the input at that exact moment, not on past or future inputs.

For example, a resistor is considered memoryless because the voltage across it at any time depends only on the current flowing through it at that same time, without considering any previous or future currents. $y(t)=Rx(t),$ where $R$ is the resistance.

A very good example of memoryless system is the identity system where the input signal is itself the output. $y[n]=x[n]$

Memory

A system has memory if the output for each value of the independent variable depends on past inputs A good example for this is the delay system where $y[n]=x[n-1].$ Here the n-1 implies the relevance of past inputs in the system thus needing the system to have memory to recall them.

Another example is a summer or accumulator which is represented by $y[n]={\sum }_{k=-\infty }^{n}x[k],$ In essence, a system has memory if it keeps track of past inputs to determine the current output. For instance, a delay system remembers previous input values, while an accumulator retains a running total of past inputs. So, an accumulator’s output at any moment depends on the sum of all previous inputs up to that time.

A capacitor is an example of a continuous-time system with memory, since if the input is taken to be the current and the output is the voltage, then $y(t)=\frac{1}{C}{\int }_{-\infty }^{t}x(\tau )d\tau ,$ where C is the capacitance. A capacitor is simply an accumulator of charge thus making it store the data of the charge.

Invertible Systems

A system is said to be invertible if distinct inputs lead to distinct outputs. Just like the one to one relations in algebra.

An example of an invertible continuous-time system is $y(t)=2x(t)$ for which the inverse ct system is $w(t)=1/2y(t)$

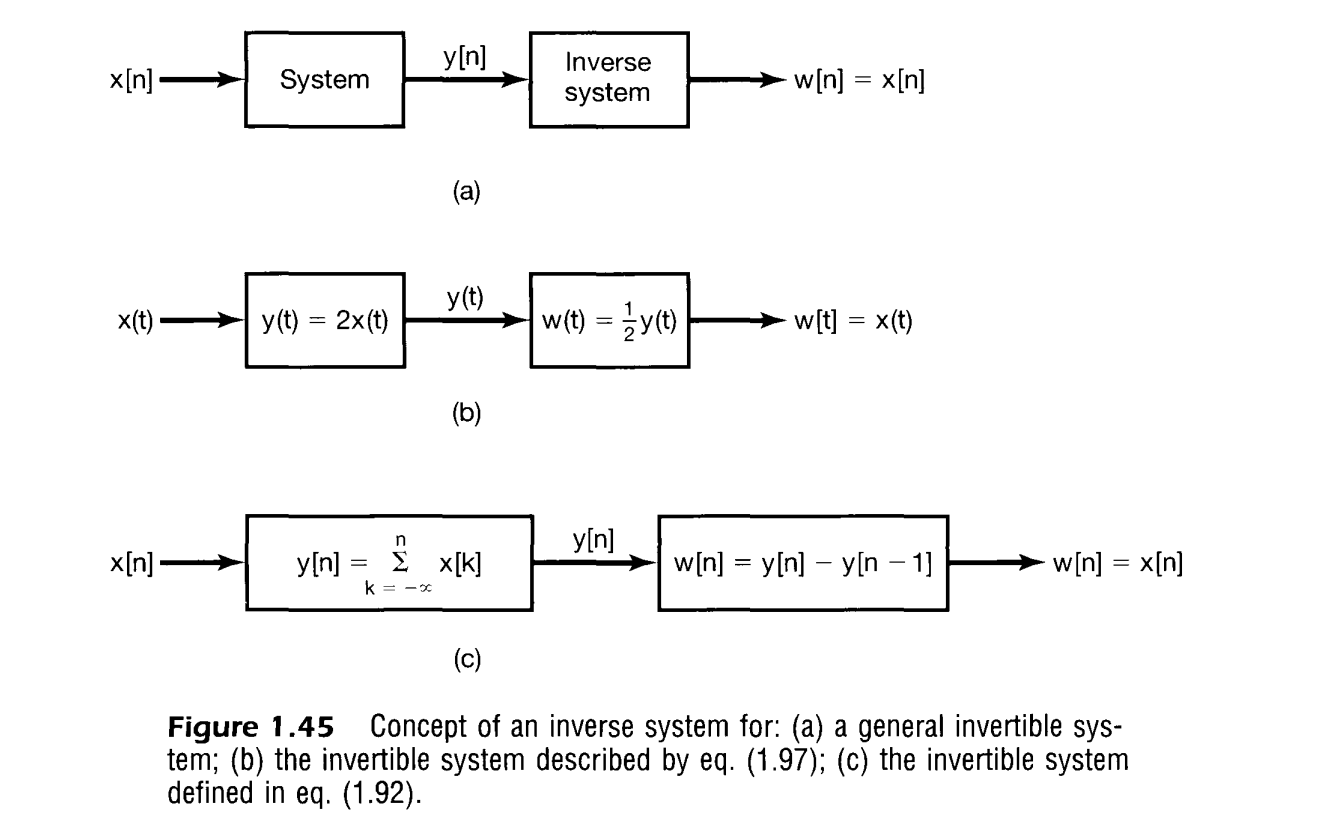
Causal Systems

A system is causal if the output at any time depends only on values of the input at the present time and in the past.

Such a system is called nonanticipative as they don’t look out for the future inputs.

For example a capacitor and resistor circuit would be causal as they only refer to the present and past values and don’t depend on future values. Refer Capacitor as an accumulator

All memory less systems are causal, since the output responds only to the current value of the input.

Examples of non causal systems

$y[n]=x[n]-x[n+1]$

Anti Causal

Anti causal signals is a special case of non causal where all the data is there only for $t\le 0$

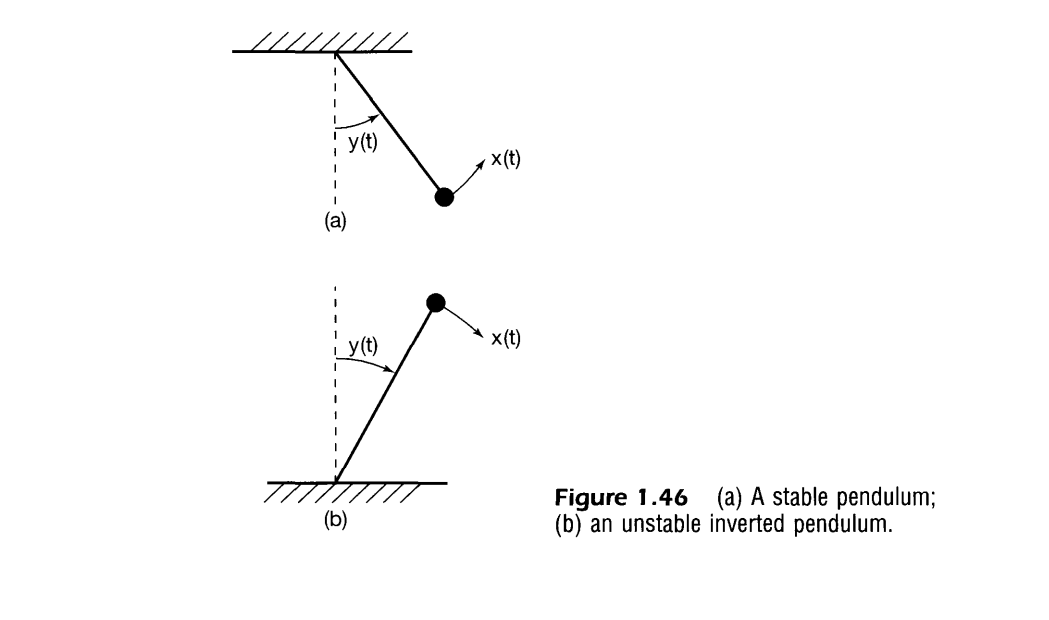
Stability

A stable system is one where the small inputs lead to responses that are not divergent. Thus small inputs leading to bounded outputs = Stable system.

For example a pendulum where the force is applied $x(t)$ and the output is angular deviation $y(t)$ from the vertical. However if one flips this pendulum they will get a very unstable output. There are also numerous examples of stable systems. Stability of physical systems generally results from the presence of mechanisms that dissipate energy. For example, assuming positive component values in the simple RC circuit of Example 1.8, the resistor dissipates energy and this circuit is a stable system. The system in Example 1.9 is also stable because of the dissipation of energy through friction.

As another example, consider the discrete-time system defined by eq. (1.1 04 ), and suppose that the input x[n] is bounded in magnit~de by some number, say, B, for all values of n. Then the largest possible magnitude for y[n] is also B, because y[n] is the average of a finite set of values of the input. Therefore, y[n] is bounded and the system is stable. On the other hand, consider the accumulator described by eq. (1.92). Unlike the system in eq. ( 1.104 ), this system sums all of the past values of the input rather than just a finite set of values, and the system is unstable, since the sum can grow continually even if x[n] is bounded $y[n]={\sum }_{k=-\infty }^{n}u[k]=(n+1)u[n].$

Time Invariance

Conceptually, a system is time invariant if the behavior and characteristics of the system are fixed over time. resistance and capacitance values R and C are constant over time and are good examples.

A system is considered time invariant if a time shift in the input signal results in an identical time shift in the output signal. Specifically, if $y[n]$ is the output of a discrete-time, time-invariant system when $x[n]$ is the input, then $y[n-n_0]$ is the output when $x[n-n_0]$ is applied. In continuous time, with $y(t)$ being the output corresponding to the input $x(t)$, a time-invariant system will produce $y(t-t_0)$ as the output when $x(t-t_0)$ is the input.

Discrete Time Invariance

The representation of Discrete Time Signals in terms of Impulses A single discrete Unit Impulse can construct an entire discrete signal.

References

Page 88 Cartesian Formulaes

Information

• date: 2024.08.20
• time: 06:15