Continued from Signals & Systems Intro

Signals & System Transformation of the independent variable

A central concept in signal and system analysis is that of the transformation of a signal. For example, in an aircraft control system, signals corresponding to the actions of the pilot are transformed by electrical and mechanical systems into changes in aircraft thrust or the positions of aircraft control surfaces such as the rudder or ailerons, which in tum are transformed through the dynamics and kinematics of the vehicle into changes in aircraft velocity and heading.

Also, in a high-fidelity audio system, an input signal representing music as recorded on a cassette or compact disc is modified in order to enhance desirable characteristics, to remove recording noise, or to balance the several components of the signal (e.g., treble and bass).

In short

We focus on a very limited but important class of elementary signal transformations that involve simple modification of the independent variable, i.e., the time axis.

The main types of transformations

Time Shift

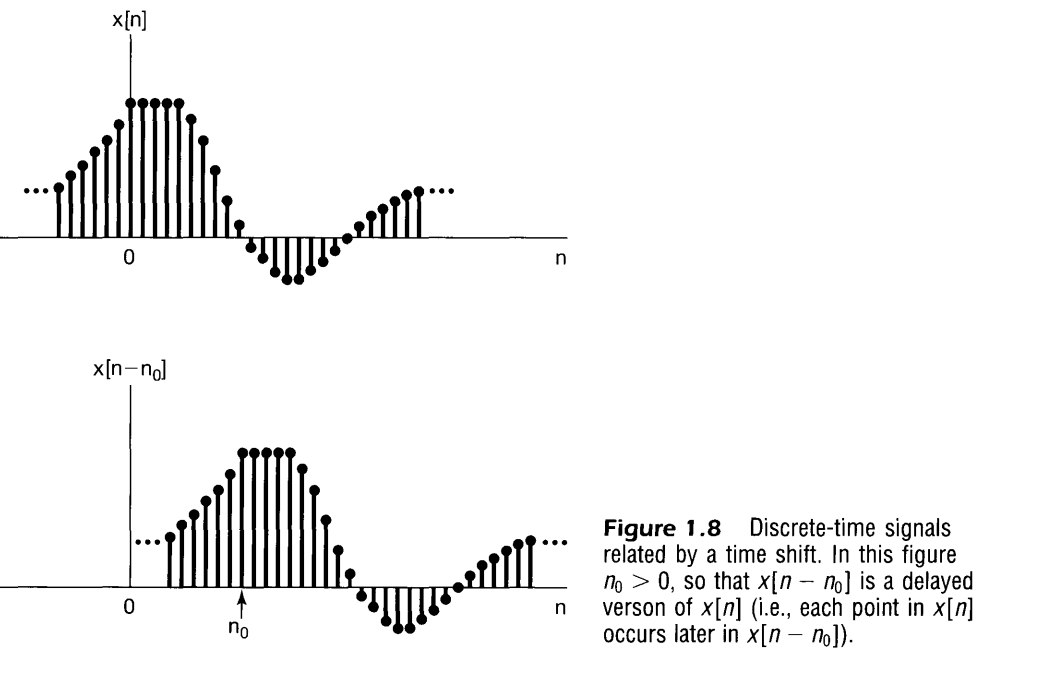
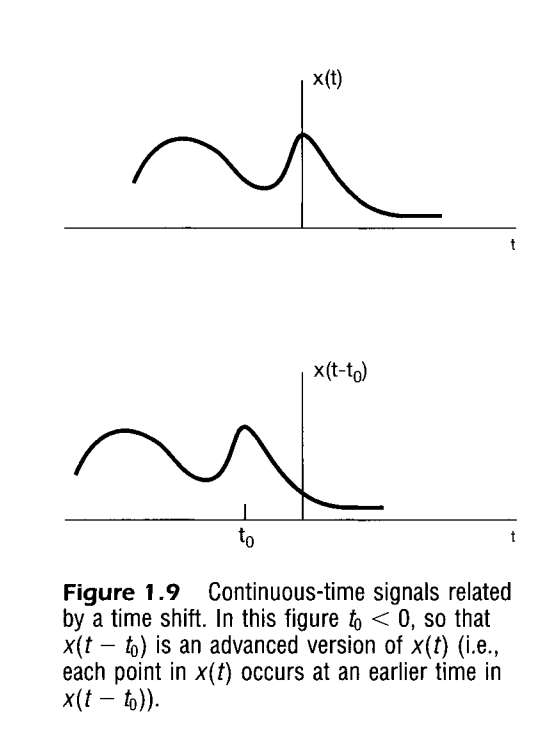
A simple and very important example of transforming the independent variable of a signal is a time shift. A time shift in discrete time is illustrated in Figure 1.8, in which we have two signals $x[n]$ and $x[n-n0]$ that are identical in shape, but that are displaced or shifted relative to each other.

Time Reversal

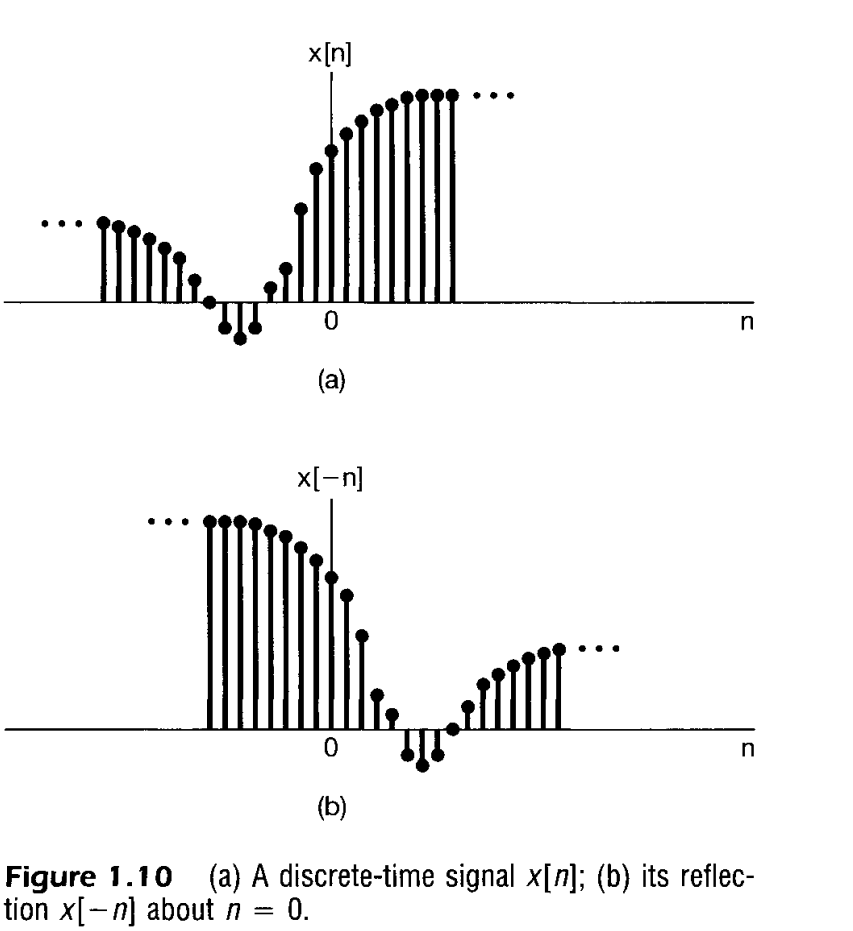
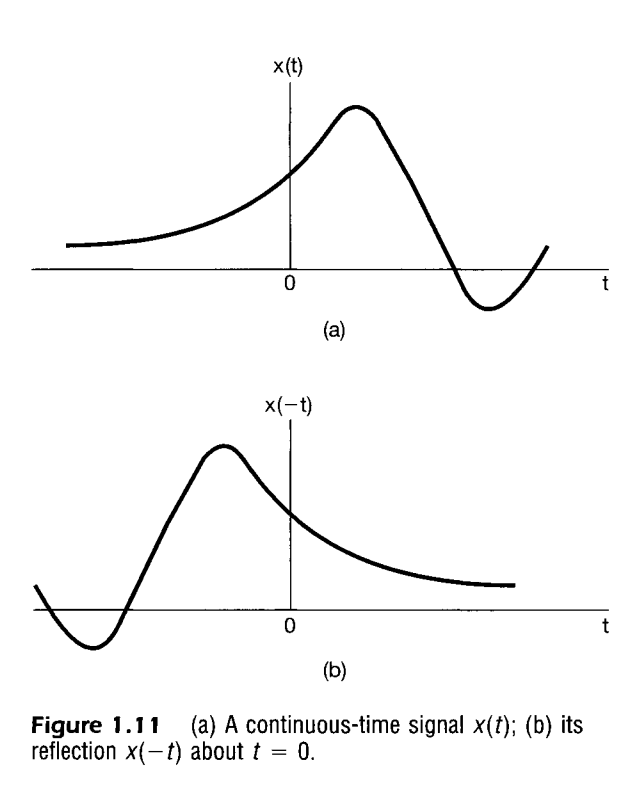
Time reversal is a fundamental signal transformation that involves flipping a signal around the vertical axis of time. For a discrete-time signal $x[n]$, time reversal results in a new signal $x[-n]$. This operation mirrors the signal’s values about the vertical axis, effectively reversing the order in which the signal values are encountered.

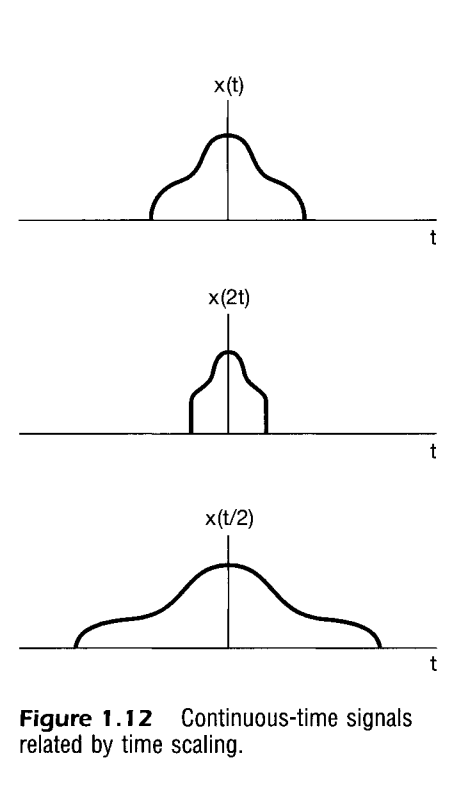
Time Scaling

Time scaling is a way to in a way change the magnification or the spectrum of time covered of a signals defined with a function. To understand graphically one can Imagine $x(t)$ as shown in the figure to be shrunk when its parameters are multiplied with $2$ such as $x(2t)$. Another way is shown where doing the vice versa i.e dividing with $2$ gets us a broader signal covering more time.

Periodic Signals

An important class of signals that we will encounter frequently throughout this book is the class of periodic signals.

Continuous

A periodic continuous-time signal x(t) has the property that there is a positive value of T for which

An important class of signals that is studied upon is a class of periodic Signals. A periodic continuous time signal $x(t)$ has the property that there is a positive value of T for which $x(t)=x(t+T)$ for all the values of $t$.

Explained in the most simplest way ever. Say a signal that remains unchanged if we add a certain amount of time $T$. That signal is periodic with period $T$.

Discrete

Periodic signals are defined analogously in discrete time. Specifically, a discrete- time signal $x[n]$ is periodic with period $N$, where $N$ is a positive integer, if it is unchanged by a time shift of $N$, i.e., if $x[n]=x[n+N]$

Example

\text{Let us illustrate the type of problem solving that may be required in determining} \\ \text{whether or not a given signal is periodic. The signal whose periodicity we wish to check is given by} \\ x(t) = \left\{ \begin{array}{ll} \cos(t) & \text{if } t < 0 \\ \sin(t) & \text{if } t \geq 0 \end{array} \right. \\ \text{From trigonometry, we know that } \cos(t + 2\pi) = \cos(t) \text{ and } \sin(t + 2\pi) = \sin(t). \text{ Thus, considering } t > 0 \text{ and } t < 0 \text{ separately, we see that } x(t) \text{ does repeat itself over every interval of length } 2\pi. \\ \text{However, as illustrated in Figure 1.6, } x(t) \text{ also has a discontinuity at the time origin that does not recur at any other time. Since every feature in the shape of a periodic signal must recur periodically, we conclude that the signal } x(t) \text{ is not periodic.} \end{array}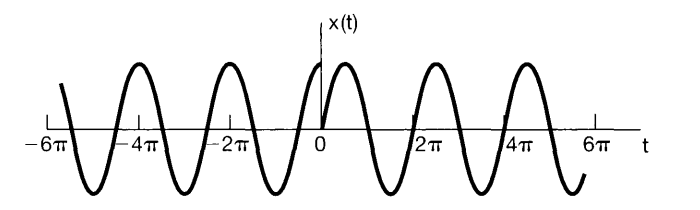

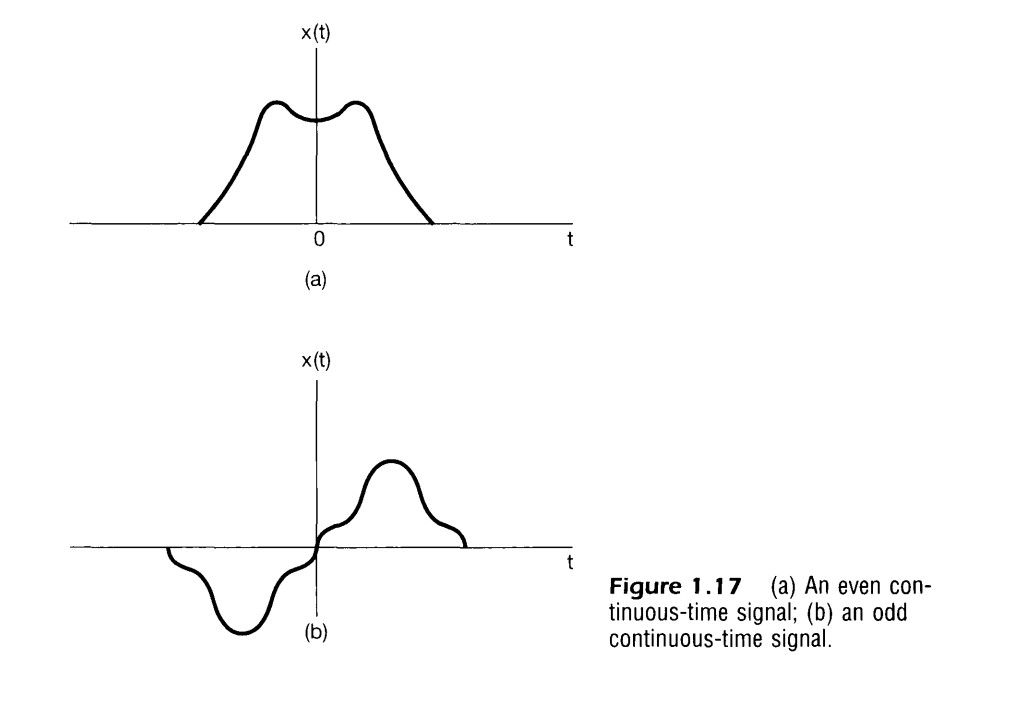
Even and Odd Signals

Another important aspect of signals is their symmetry under time reversal.

Even

A signal $x(t)$ or $x[n]$ is referred to as an even signal if it is identical to its time-reversed counterpart, i.e., with its reflection about the origin. In continuous time a signal is even if $x(-t)=x(t),$ while a discrete-time signal is even if $x[-n]=x[n].$

Odd

A signal is referred to as odd if $\begin{array}{r}x(-t)=-x(t),\\ x[-n]=-x[n].\end{array}$ An odd signal must necessarily be $0$ at $t=0$ or $n=0$. This is simply because $x(0)=-x(0)$ or $x[0]=-x[0]$

Finding Even and Odd Parts

Any signal can be broken into parts which represent even and odd parts

Even Part

$\mathcal{E}\nu \left[x(t)\right]=\frac{1}{2}\left[x(t)+x(-t)\right],$

Odd Part

$\Theta d\{x(t)\}=\frac{1}{2}[x(t)-x(-t)].$

References

S&S Oppenheim Continued to Signals and Systems Exponentials and Sinusoidals

Information

• date: 2024.08.20
• time: 01:42