Signals & Systems Intro

1. Signals And System

Introduction

1. Introduction to Signals and Systems:

   • Contextual Background:
     • Signals and systems have intuitive notions that appear in a wide range of contexts.
     • An analytical framework is used to describe and analyze signals and systems.

2. Analytical Framework:

   • Purpose:
     • Provides a language for describing signals and systems.
     • Offers a powerful set of tools for analysis.
   • Applicability:
     • The framework is versatile and applies to problems across various fields.

3. Mathematical Description and Representations:

   • Foundation:
     • This chapter introduces the mathematical foundations for signals and systems.
     • Key mathematical descriptions and representations will be covered.

4. Development of Additional Concepts:

   • Building on the Foundation:
     • Subsequent chapters will expand on the basic concepts introduced.
     • Additional methods and concepts will be developed to enhance understanding and problem-solving capabilities.

5. Applications:

   • Broad Array of Applications:
     • The concepts and methods are relevant to a wide range of practical applications.
     • The goal is to improve the ability to analyze and solve problems involving signals and systems.

Summary:

• The introductory chapter sets up the mathematical groundwork for signals and systems.
• It highlights the importance of a strong analytical framework for understanding and solving related problems.
• Subsequent chapters will build on this foundation to explore more complex concepts and applications.

Continuous & Discrete Time Signals

Signals can depict various physical phenomena. All the information in a signal is captured in patterns of some form.

Example 1 Audio

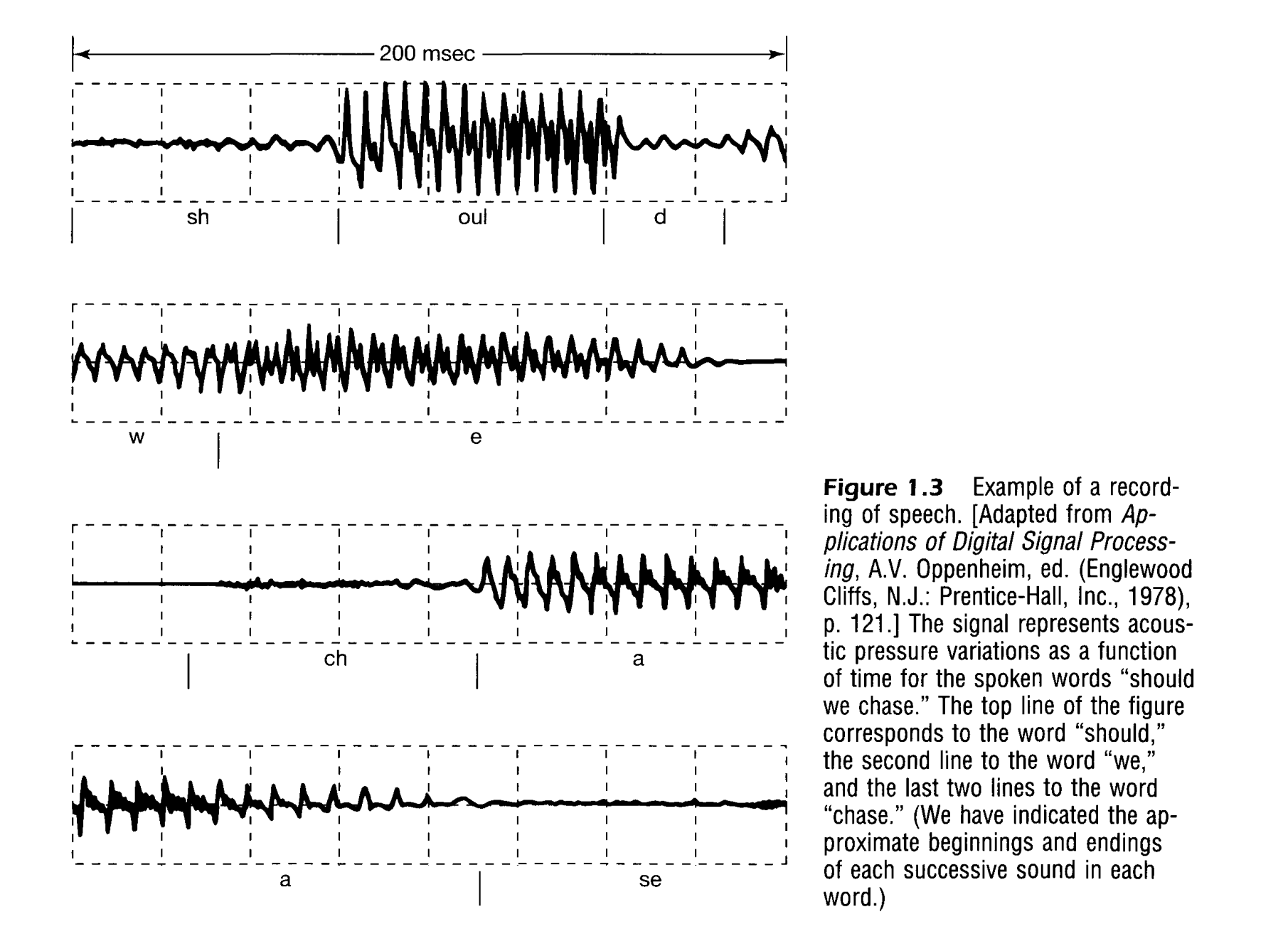
Explanation

In this figure 1.3 The acoustic vibrations are recorded by a device which converts it into electronic signal. This electronic signal. Different sounds make different patterns. Thus we can see the variation.

Example 2

This is figure depicts the representation of image brightness values. This is a monochromatic image. More on this later.

Signals

Signals are represented mathematically as functions of one or more independent variables.

A speech signal can be represented mathematically by acoustic functions of time and Pressure. Time and Pressure here are both independent variables.

A picture can be represented by a brightness function of two spatial variables.

In our current context we will only look at one single independent variable. For Convenience we will be focusing on time $t$.

But they are various signals that are not dependent on time for example this one right here. ^1

---

Things to lookout

Throughout the book we will be considering two basic type of signals: continuous time signals and discrete-time signals. A speech signal as a function of time and atmospheric pressure as a function of altitude are examples of continuous-time signals.

Continuous Signal

Throughout this book we will be considering two basic types of signals: continuous time signals and discrete-time signals. In the case of continuous-time signals the independent variable is continuous, and thus these signals are defined for a continuum of values of the independent variable.

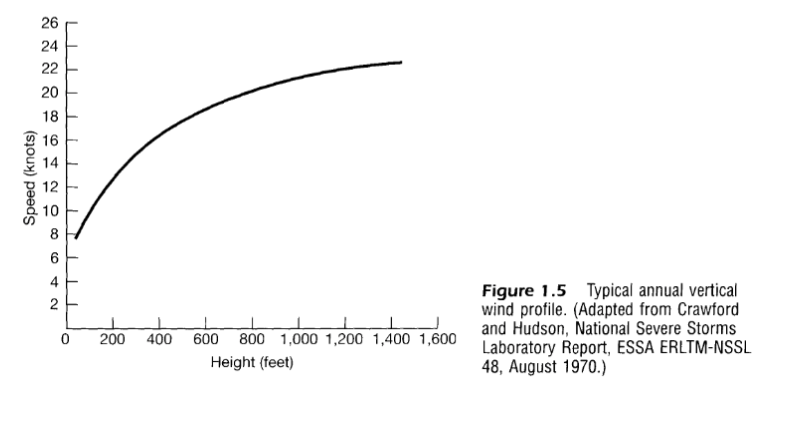
A speech signal as a function of time and atmospheric pressure as a function of altitude are examples of continuous-time signals. Refer Figure 1.5

Discrete Signal

On the other hand, discrete-time signals are defined only at discrete times, and consequently, for these signals, the independent variable takes on only a discrete set of values.

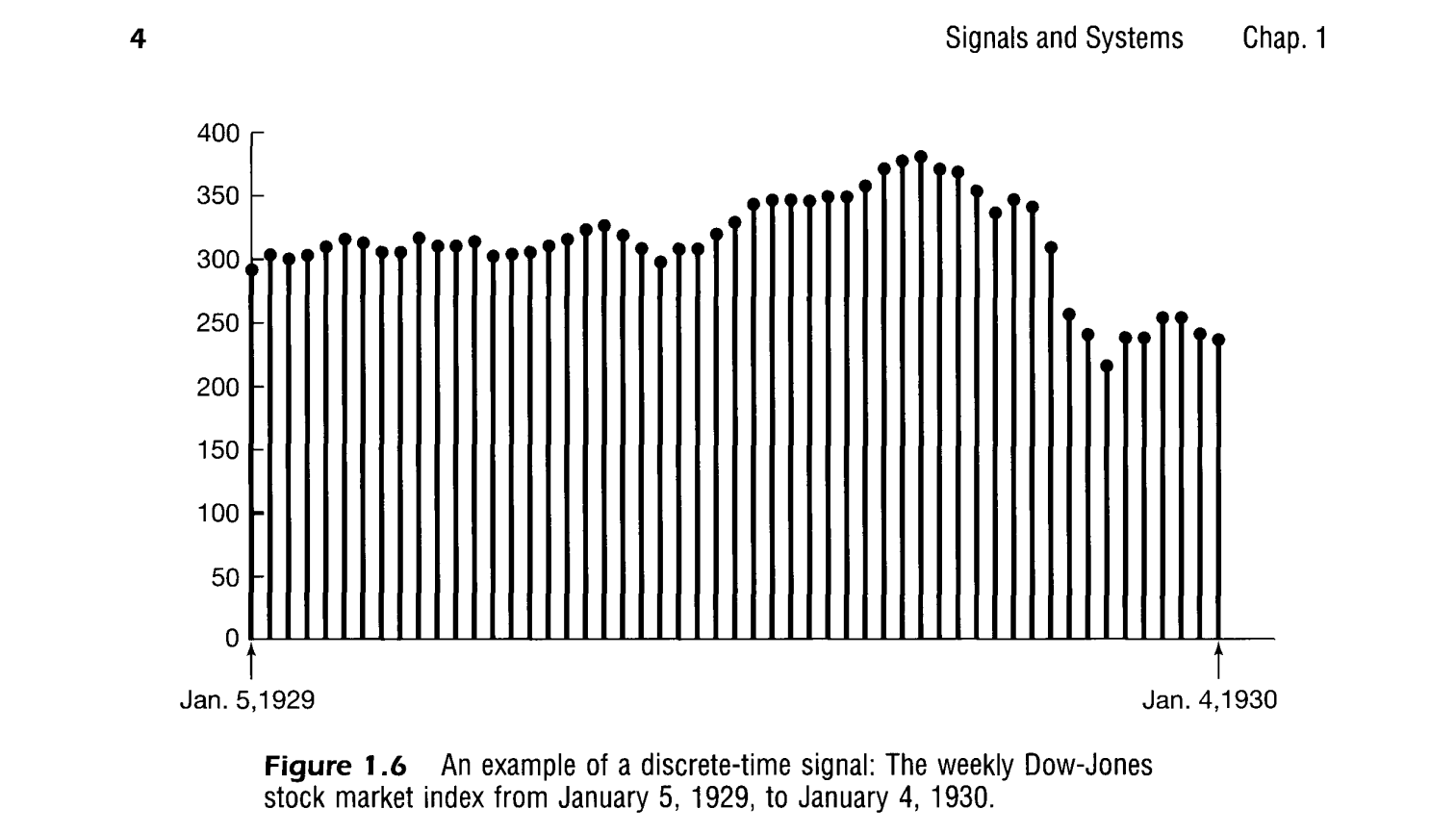
The weekly Dow-Jones stock market index, as illustrated in Figure 1.6, is an example of a discrete-time signal.

Other examples of discrete-time signals can be found in demographic studies in which various attributes, such as average budget, crime rate, or pounds of fish caught, are tabulated against such discrete variables as family size, total population, or type of fishing vessel, respectively

A Discrete Time Signal $x[n]$ may represent a phenomenon for which the independent variable is inherently discrete. Signals such as demographic data are example of this.

Most of the Discrete Signals are made from sampling of continuous time signals. In this case, the discrete-time signal $x[n]$ represents successive samples of an underlying phenomenon for which the independent variable is continuous.

Sampling: The process of converting a continuous-time signal into a discrete-time signal involves taking samples at specific intervals. Each sample represents the signal’s value at a particular point.

Integer Indexing: The discrete-time signal $x[n]$ is defined only at integer values of $n$. This is analogous to how you can’t reference a fractional sample in a digital signal, similar to how you wouldn’t discuss a family budget in terms of a fraction of a family member.

How to differentiate between these?

To differentiate between Continuous Signals and Disc

To distinguish between Continuous-Signal and discrete-time signals, we will use the symbol $t$ to denote the continuous-time independent variable and $n$ to denote the discrete time independent variable.

In addition, for continuous-time signals we will enclose the independent variable in parentheses $(\cdot )$, whereas for discrete-time signals we will use brackets $[\cdot ]$ to enclose the independent variable.

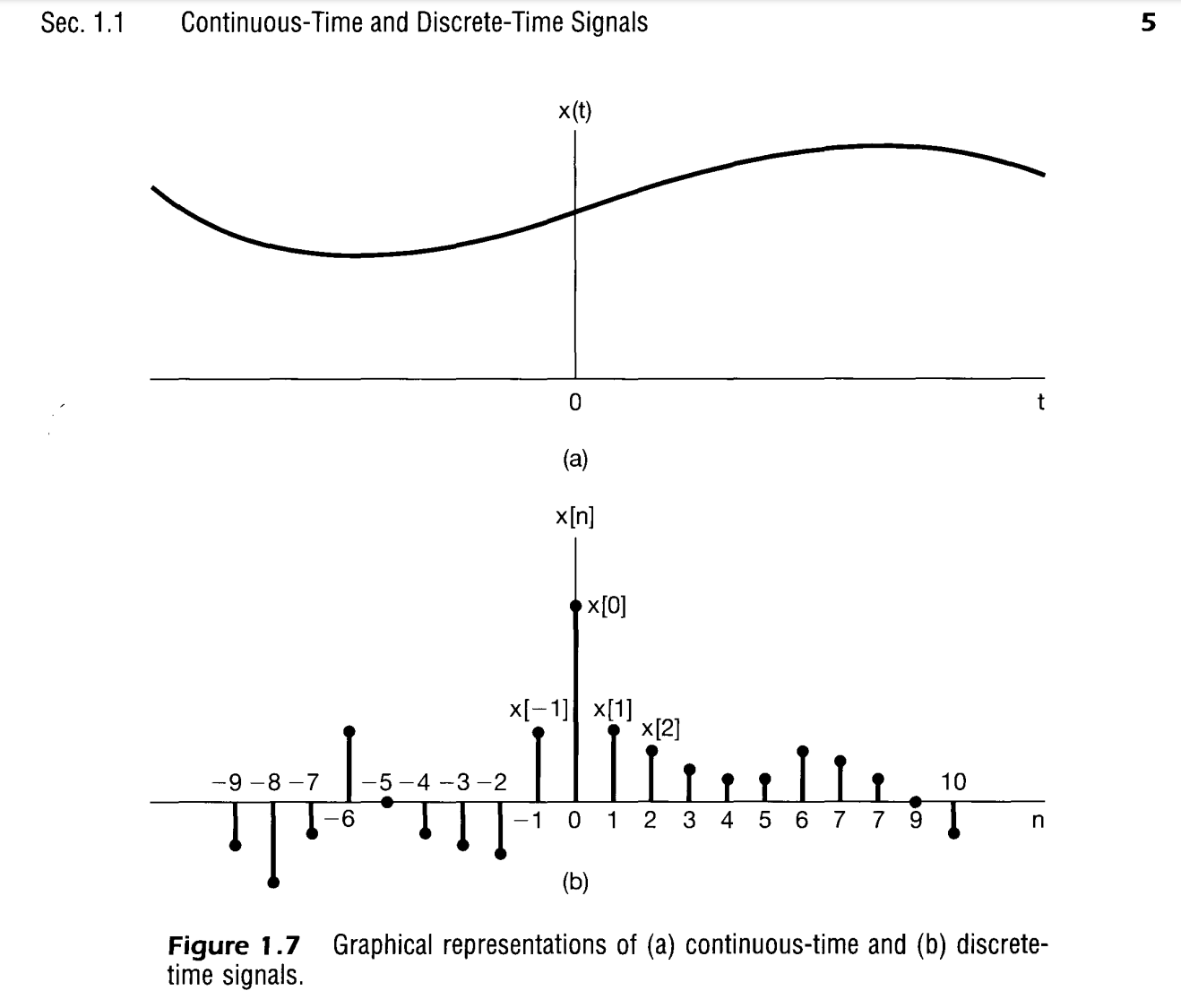
We will also have frequent occasions when it will be useful to represent signals graphically. Illustrations of a continuous-time signal $x(t)$ and a discrete-time signal $x[n]$ are shown in Figure 1.7. It is important to note that the discrete-time signal $x[n]$ is defined only for integer values of the independent variable. Our choice of graphical representation for $x[n]$ emphasizes this fact, and for further emphasis we will on occasion refer to $x[n]$ as a discrete-time sequence.

Signal Energy And Power

From the range of examples provided so far, we see that signals may represent a broad variety of phenomena. In many, but not all, applications, the signals we consider are di- rectly related to physical quantities capturing power and energy in a physical system. For example, if v(t) and i(t) are, respectively, the voltage and current across a resistor with resistance R, then the instantaneous power is $p(t)=\nu (t)i(t)=\frac{1}{R}{\nu }^2(t).$ $\begin{array}{c}\mathrm{The}\mathrm{total}energy\mathrm{expended}\mathrm{over}\mathrm{the}\mathrm{time}\mathrm{interval}{t}_1\le t\le t_2\mathrm{is}\\ {\int }_{t_1}^{t_2}p(t)dt={\int }_{t_1}^{t_2}\frac{1}{R}{v}^2(t)dt,\\ \mathrm{and}\mathrm{the}averagepower\mathrm{over}\mathrm{this}\mathrm{time}\mathrm{interval}\mathrm{is}\\ \frac{1}{t_2-t_1}{\int }_{t_1}^{t_2}p(t)dt=\frac{1}{t_2-t_1}{\int }_{t_1}^{t_2}\frac{1}{R}{v}^2(t)dt.\end{array}$

Continue reading Signals & System Transformation of the independent variable for further studies

References

S&S Oppenheim

Continued to Signals & System Transformation of the independent variable

Information

• date: 2024.08.19
• time: 15:02