kw# Djikstra’s Algorithm
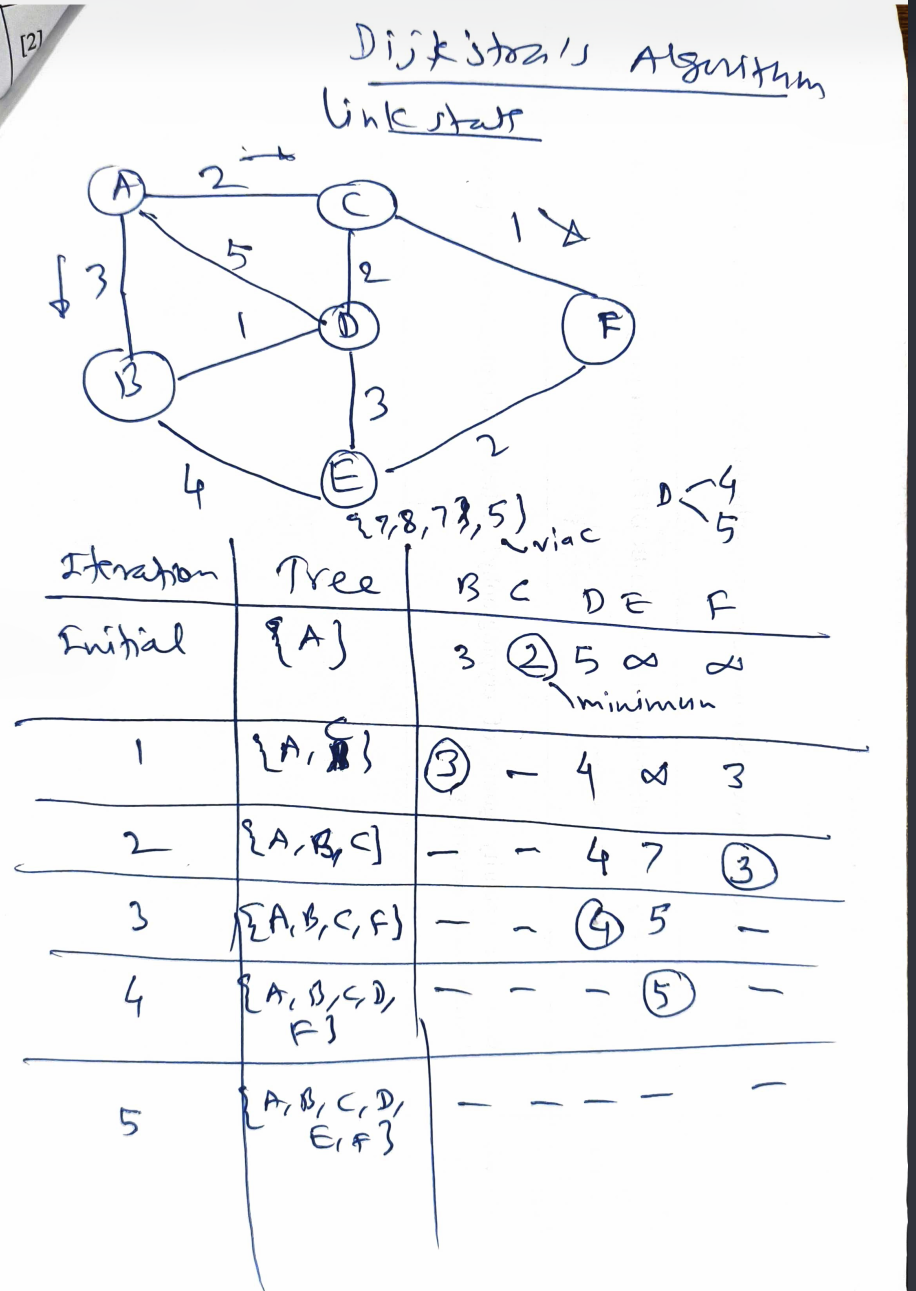This image shows a detailed illustration of Dijkstra’s Algorithm, which is used to find the shortest paths from a starting node (node A in this case) to all other nodes in a graph. It is often used in routing and link-state protocols, such as Link-State Routing.
Let me walk you through the elements in this diagram and explain how Dijkstra’s Algorithm works step by step.
1. The Graph
The graph shown in the diagram consists of six nodes: A, B, C, D, E, F. The edges between these nodes have weights, which represent the cost or distance between two directly connected nodes.
Here’s a summary of the graph’s edges:
- A → B: Cost is 3
- A → C: Cost is 2
- B → D: Cost is 4
- C → D: Cost is 1
- C → F: Cost is 4
- D → E: Cost is 3
- E → F: Cost is 2
2. The Table Structure
The table in the diagram shows the process of Dijkstra’s Algorithm iteration by iteration. Here’s what each part of the table represents:
- Iteration: Shows the steps of the algorithm. The algorithm adds one node to the shortest path tree in each iteration.
- Tree: Represents the set of nodes that have been added to the shortest path tree at that step.
- The columns B, C, D, E, F: Show the current shortest known distance from the starting node (A) to each of these nodes at the particular step.
- The values in parentheses indicate the current distance to a node. If the distance is infinity (∞), it means that the node has not been reached yet.
Dijkstra’s Algorithm - Step by Step
Let’s break down the iterations shown in the diagram.
Initial Step:
-
Tree:
{A}(starting node is A). -
B, C, D, E, F: Initial distances from A to other nodes:
- A → B = 3 (direct edge)
- A → C = 2 (direct edge)
- A → D, E, F = ∞ (no direct path known yet)
-
So, initially, the shortest known path from A is:
- A → B = 3
- A → C = 2
- A → D, E, F = ∞
The algorithm chooses the node with the smallest distance that hasn’t been added to the tree yet, which is C (cost = 2).
Iteration 1:
- Tree:
{A, C}(C is added since it’s the closest). - Now, update the distances to the other nodes based on node C:
- From C → D, the cost is 2 + 1 = 3 (A → C → D).
- From C → F, the cost is 2 + 4 = 6 (A → C → F).
- The distance to B remains unchanged at 3.
- So now, the shortest known path distances are:
- A → B = 3
- A → C = 2
- A → D = 3
- A → F = 6
- A → E = ∞
- B and D both have a distance of 3, so the algorithm can choose either. In this case, B is chosen.
Iteration 2:
- Tree:
{A, B, C}(B is added). - The distances are updated based on node B:
- From B → D, the cost is 3 + 4 = 7, but the existing distance to D through C is shorter (A → C → D = 3), so no update is made.
- The other distances remain the same:
- A → B = 3
- A → C = 2
- A → D = 3
- A → F = 6
- A → E = ∞
- The algorithm now chooses D because it has the smallest distance (3).
Iteration 3:
- Tree:
{A, B, C, D}(D is added). - The distances are updated based on node D:
- From D → E, the cost is 3 + 3 = 6 (A → C → D → E).
- The distance to F stays 6.
- So now, the shortest known path distances are:
- A → B = 3
- A → C = 2
- A → D = 3
- A → E = 6
- A → F = 6
- Now the algorithm can choose either E or F (both have a distance of 6), so F is chosen in this iteration.
Iteration 4:
- Tree:
{A, B, C, D, F}(F is added). - Since all remaining nodes already have updated distances, no changes occur in the table:
- A → B = 3
- A → C = 2
- A → D = 3
- A → E = 6
- A → F = 6
- The only remaining node is E, which is added in the next iteration.
Iteration 5:
- Tree:
{A, B, C, D, E, F}(all nodes are added to the tree). - The algorithm completes since all nodes have been processed and the shortest paths are found.
Final Shortest Path Tree:
After all iterations, the shortest paths from A to all other nodes are as follows:
- A → C = 2
- A → B = 3
- A → D = 3 (via C)
- A → E = 6 (via D)
- A → F = 6 (via C)
Summary of the Steps:
- Dijkstra’s Algorithm works by iteratively adding the closest (minimum distance) node to the shortest path tree and updating the distances to its neighboring nodes.
- The algorithm guarantees that, once a node is added to the tree, the shortest path to that node is found.
- The table helps to track the current shortest distance from the source node A to each other node at each step of the algorithm.
Let me know if you’d like further clarification on any part!
References
Information
- date: 2024.10.07
- time: 07:22